因子分解机的基础和进阶
- 什么是因子分解机?
- 因子分解机的定义
- 因子分解机的复杂度分析
- 因子分解机有什么用?
- 如何实现因子分解机?
- 参考文献
什么是因子分解机?
因子分解机的定义 (Define)
FM(Factorization Machine) 是由Konstanz大学Steffen Rendle 在 2010年提出的$^{[1]}$,目的是为了解决稀疏数据(sparsity data)下的特征组合问题。下面我们通过几个栗子来看看什么是因子分解机。
例一$^{[3]}$:
我们观测到的数据的图表形式如下:
| rating | User | Movie | rate-date | … |
|---|---|---|---|---|
| 5 | Alice | Titanic | 2010-1 | … |
| 4 | Bob | Notting Hill | 2010-2 | … |
| 3 | Charlie | Star War | 2009-12 | … |
这个例子是一个电影评分系统数据集。考虑电影评分系统种的数据,它的每一条记录都包含了哪个用户 $u \in U$在什么时候$t \in R$,对哪部电影$i \in I$打了多少分$r \in {1,2,3,4,5}$ 这样的信息。
数据集S的列表形式就是:
$S = { (Alice, Titanic, 2010-1, 5), (Bob, Notting Hill, 2010-2, 4)}$
那么我可以使用数据集S来进行预测任务、推荐等任务,比如找到一个函数$\hat{y}$来预测某个用户在某个时刻对某个电影的打分行为。
有了数据集S,通过下图的方式,我们可以构建一个特征向量和标签的示例:
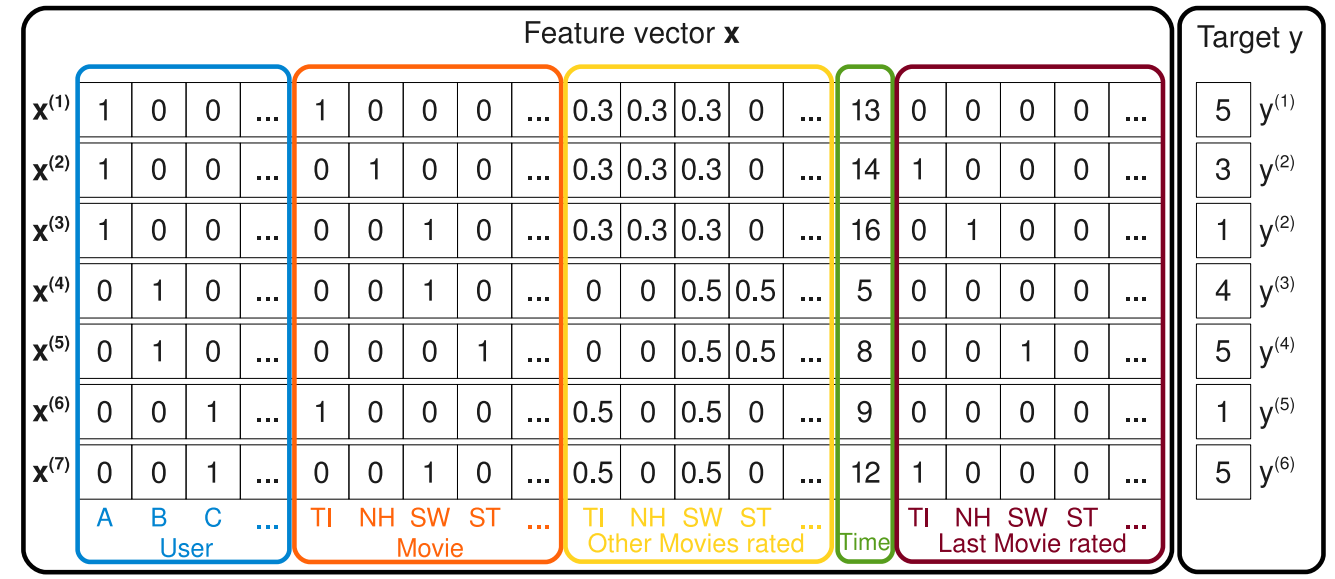
上图中的标签部分比较简单,就是直接的让当前用户对电影的评分作为标签,比如第一条测试记录中Alice 对 Titanic的评分是 5,那么$y^{(1)} = 5$,而特征向量$X$由以下五部分组成:
1、第一部分(蓝色方框)表征的是当前评分用户的信息,其维度为$|U|$,这里使用的是One-hot Encoding的方法。也就是除了当前位置是1,其余位置都是0。
2、第二部分(红色方框)表征的是当前被评分电影信息,其维度为$|I|$,这里使用的也是One-hot Encoding的方法。
3、第三部分(黄色方框)表征的是当前评分用户评分过的所有电影信息,其维度是$|I|$,假设当前用户评论过的电影个数为$n_I$,那么这$n_I$个电影位置上的数值为$\frac{1}{n_I}$,其他位置上都是0。
4、第四部分(绿色方框)表征的是评分日期信息,维度为1,我们将最早的记录日期——2009年1月开始基数为1,以后没增加一个月,就加一,比如2009年5月就是5。
5、第五部分(棕色方框)表征的是当前评分用户最近评分过的一部电影的信息,其维度为$|I|$,同样的也是使用One-hot Encoding的方法。比如Alice现在评价的是Titanic,之前还评价过一次Notting Hill,那么Notting Hill位置的为1,其余为0,如果之前没有评价过任何电影,就全部取0。
所以,X的总维度是 $|U| + |I| + |I| + 1 + |I| = |U| + 3|I| + 1$
显然,在一个真实的电影评分系统中,用户的数目$|U|$和电影的数目$|I|$通常是很大的,而每个用户参与评论的电影数目则相对而言比较小。于是,对于每一条记录对应的特征向量将会非常的稀疏。
所以,我们需要有一个办法来降低这种稀疏性。
例二$^{[2]}$:
假设一个广告分类的问题,根据用户和广告位相关的特征,预测用户是否点击了广告。源数据如下:
| Clicked? | Country | Day | Ad_type |
|---|---|---|---|
| 1 | USA | 3/3/15 | Movie |
| 0 | China | 1/7/14 | Game |
| 1 | China | 3/3/15 | Game |
“Clicked?”是label,Country、Day、Ad_type是特征。由于三种特征都是categorical类型的,需要经过(One-Hot Encoding)转换成数值型特征。
| Clicked? | USA | China | 26/11/15 | 1/7/14 | 19/2/15 | Movie | Game |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
从上面那张表。可以看出,我们在使用了One-hot Encoding之后,显然也会出现跟例一中一样的问题,那就是稀疏性非常明显。
同时,我们观察数据样本,也可以发现,有一些特征,相互关联之后,跟label的相关性也会提升。
比如“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的有很强关联性的特征,它们对用户是否点击,会产生正面的影响。
用一个小例子来解释就是:来自“China”的用户在“Chinese New Year”这一天会有大量的浏览、购买行为,但是再“Thanksgiving”这天,却不会有特别的消费行为。相反地是,来自“USA”的用户很可能在“Thanksgiving”这天有大量的浏览、购买行为,但是在“Chinese New Year”却可能没有特别的消费行为。
这种关联特征与label的正向相关性在实际问题中是普遍存在的,如“化妆品”类商品与“女”性,“球类运动配件”的商品与“男”性,“电影票”的商品与“电影”品类偏好等。因此,引入两个特征的组合是非常有意义的。
我们可以使用多项式来直观地表现多项式模型,让特征$x_i$和$x_j$组合,得到如下表达式,这里我们只讨论二阶多项式模型:
$$y(x) = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij} x_i x_j$$
$$= w_0 + W_1^TX + X^TW_2X \ \ \ \ \ \ (1)$$
可以看到,当$x_i$和$x_j$有一个为零,这时的组合特征$x_ix_j$是没有意义的。
其中$n$表示样本的特征数量,$x_i$表示第i个特征的值,$w_0、w_i、w_{ij}$是参数模型。
显然,我们写出这个模型的过程,并不复杂,然后我们只要能求出 $w_0、w_i、w_{ij}$就能够建立起一个很好用的,引入了组合特征的模型。
但是事实真的是这样么?这里我们依旧会遇到跟例一中,一样的问题,就是样本太少了,稀疏性太强,哪怕强行求出了$w_{ij}$,得到的模型也会是欠拟合的那种。
那么,我们如何解决这个问题呢?
一个可以想到的办法就是通过矩阵分解。
在推荐系统中,我们把一个评分矩阵,分解成一个user和一个item,每个user和item都可以采用一个隐向量表示。比如在下图中的例子中,我们把每个user表示成一个二维向量,同时把每个item表示成一个二维向量,两个向量的点积就是矩阵中user对item的打分。
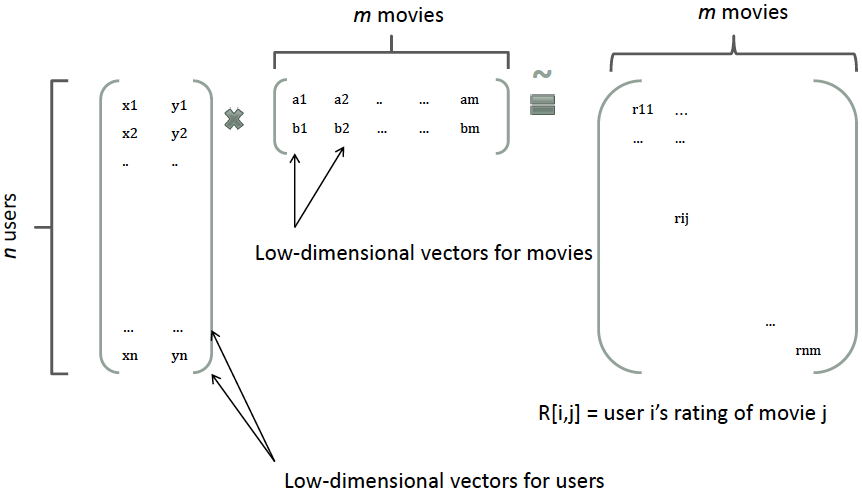
按照,这个思想,我们可以对中间的权重$W_2$做一次矩阵分解。
$$W_2 = V^TV, V \in R^{k \times n}$$
那么有
$$w_{ij} = V_i^TV_j, V_i \in R^k$$
最后公式$(1)$可以化成
$$y(\mathbf{x}) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j (2)$$
这里的$\langle \mathbf{v}_i, \mathbf{v}_j \rangle$表示的是两个长度为k的向量的点乘
$$\langle \mathbf{v}_i, \mathbf{v}j \rangle = \sum{f=1}^k v_{i,f} \cdot v_{j,f}$$
这样一来得到的隐向量的长度为$k$,包含$k$个描述特征的因子。且二次项的参数的个数就成了$kn$远远少于$n^2$。另外参数因子化使得 $x_h x_i$ 的参数和 $x_ix_j$ 的参数不再相互独立。
因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说,$x_hx_i$ 和 $x_ix_j$ 的系数分别为 $\langle v_h, v_i \rangle$ 和 $\langle v_i, v_j \rangle$,它们之间有共同项 $v_i$。也就是说,所有包含“ $x_i$ 的非零组合特征”(存在某个 $j \ne i$,使得 $x_i x_j \ne 0$ )的样本都可以用来学习隐向量 $v_i$,这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中,$w_{hi}$ 和 $w_{ij}$ 是相互独立的。
数学角度看差异
接下来,我们从数学的角度看看(1)和(2)的主要区别在哪里,对于交叉项 $x_i x_j$ 的系数,前者用的是 $w_{ij}$,后者用的是 $\hat w_{ij}$ ,为了能够更好的说明,我们引入几个矩阵。
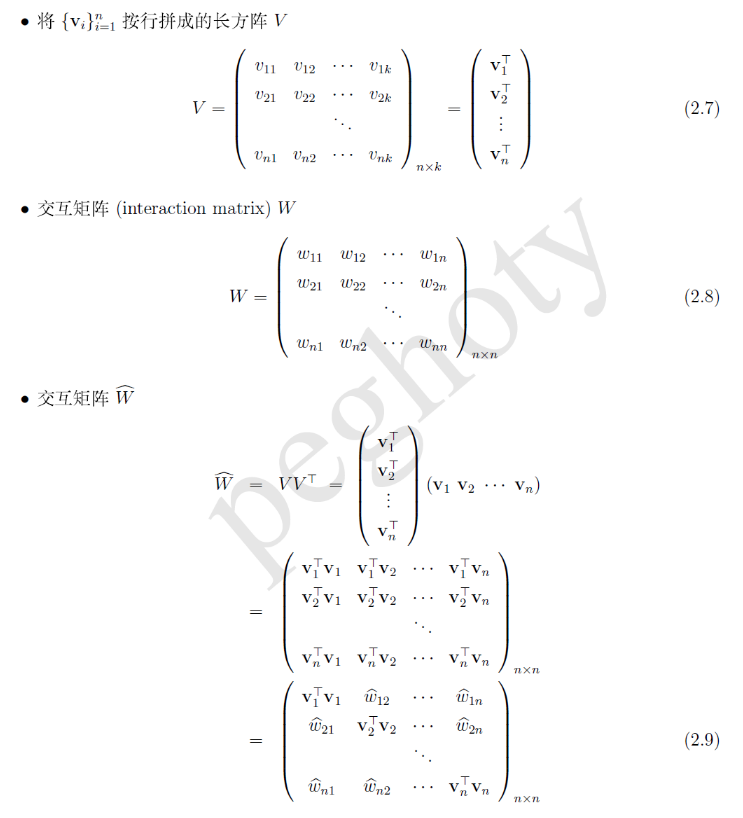
由此可见,(1) 和 (2)分别采用了交互矩阵 $W$ 和$\hat W$的非对角线元素作为$w_ix_j$的系数.由于$\hat W = VV^T$对应于一种矩阵分解,因此,我们将这种以(2)作为模型的方法称为 Factorization Machine.
这里,我们需要补充一个条件 “当k足够大的时候,对于任意对称正定的实矩阵 $\hat W \in R^{n \times k}$,会使得 $\hat W=VV^T$ 成立.
因子分解机的复杂度分析
自然,$(2)$是一个通用的拟合方程,我们可以采用不同的损失函数【我们用来对结果进行判断的函数】用于解决回归、二元分类等问题,比如:
1、 采用MSE(Mean Square Error)损失函数来求解回归问题,
2、 采用Hinge/Cross-Entropy损失来求解分类问题。
看得出来(2)的时间复杂度是$O(kn^2)$。但是,有意思的是我们通过使用一个trick,可以把时间减到$O(kn)$,具体细节证明如下,详情可以看论文$^{[3]}$
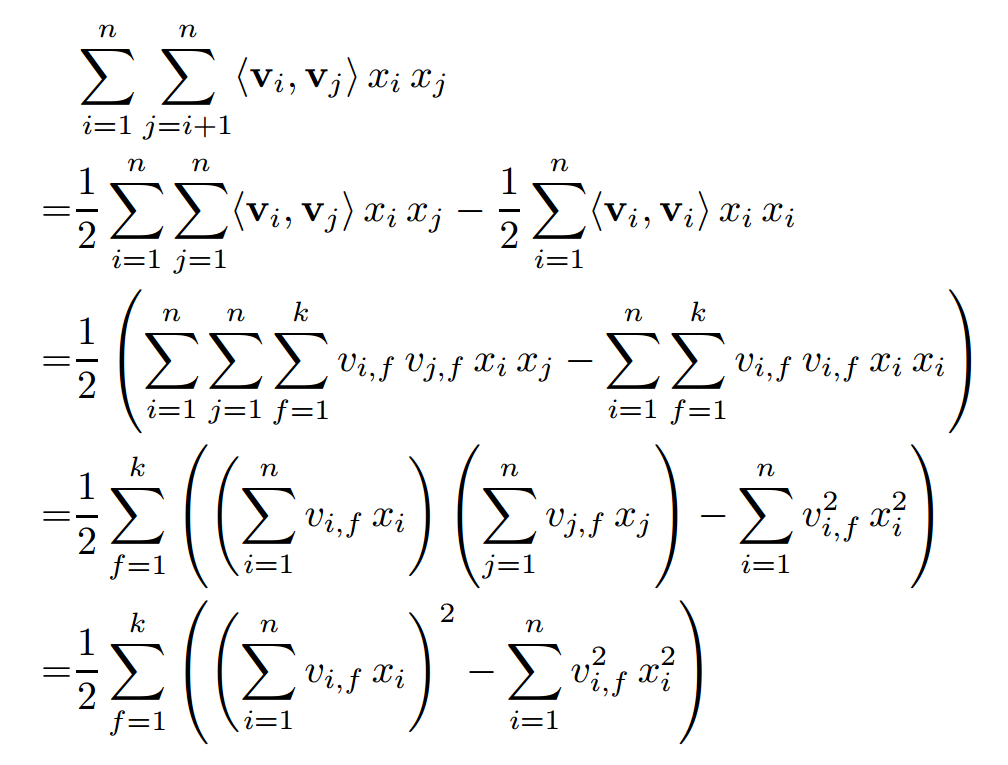
由此可见,FM可以在线性时间对新样本作出预测。
$\sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j = \frac{1}{2} \sum_{f=1}^k \left(\left( \sum_{i=1}^n v_{i, f} x_i \right)^2 - \sum_{i=1}^n v_{i, f}^2 x_i^2 \right)$
我们再来看一下FM的训练复杂度,利用SGD(Stochastic Gradient Descent)训练模型。模型各个参数的梯度如下
$$\frac{\partial}{\partial\theta} y (\mathbf{x}) = \left{\begin{array}{ll} 1, & \text{if}\; \theta\; \text{is}\; w_0 \ x_i, & \text{if}\; \theta\; \text{is}\; w_i \ x_i \sum_{j=1}^n v_{j, f} x_j - v_{i, f} x_i^2, & \text{if}\; \theta\; \text{is}\; v_{i, f} \end{array}\right.$$
其中$v_{j,f}$是隐向量$V_j$的第$f$个元素。由于$\sum_{j=1}^nv_{j,f}x_j$只与$f$有关,而与$i$无关,在每次迭代的过程中,只需要计算一次所有$f$的$\sum_{j=1}^nv_{j,f}x_j$就能够得到所有$v_{j,f}$的梯度。显然,计算所有$f$的$\sum_{j=1}^nv_{j,f}x_j$的复杂度是$O(kn)$;已知$\sum_{j=1}^nv_{j,f}x_j$时,计算每个参数梯度的复杂度时$O(1)$;得到梯度后,更新每个参数的复杂度为$O(1)$;模型参数一共有$nk + n + 1$个。因此,FM参数训练的复杂度也是$O(kn)$。综上可知,FM可以在线性时间训练和预测,是一种非常高效的模型。
因子分解机有什么用?
1、 FM和矩阵分解
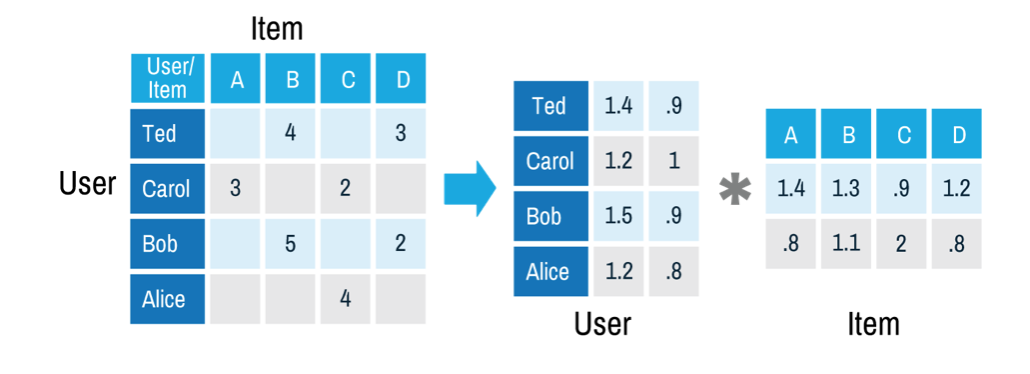
在推荐系统中,我们经常使用的就是基于矩阵分解的协同过滤$^{[4]}$,我们会使用到 user 对 Item 的评分,但是由于 user 和 item 的数量非常多,但是 user 对 item 打分的个数却十分稀少。基于矩阵分解的协同过滤就是用来预测 user 对那些没有过消费记录的 item 的打分行为,以及打多少分。实际上可以看成一个评分预测的问题。矩阵分解的方法假设 user 对 item 的打分 $\hat r_{ui}$ 由下式决定:
$$\hat r_{ui} = q_i^Tp_u + \mu + b_i + b_u$$
其中,$q_i$ 是第 $i$ 个 item 所对应的隐向量,$p_u$ 是第 $u$ 个 user 所对应的隐向量,$b_i$ 代表 item 的偏差,解释了商品本身的冷门、热门程度。 $b_u$ 代表了 user 的偏差,解释了用户本身的打分偏好,$\mu$ 是常数。也就是将评分矩阵分解为 user 矩阵、 Item 矩阵的乘积再加上线性项和常数项,且这两个矩阵都是低秩的。并且这些参数可以通过最小化经验误差得到:
$$\min_{p,q,b} \sum_{u,i \in K}(r_{ui} - \hat r_{ui})^2 + \lambda(||p_u||^2 + ||q_i||^2 + b_u^2 + b_i^2)$$
从上面的叙述来看,FM的二阶矩阵也使用了矩阵分解的技巧,那么基于矩阵分解的协同过滤和FM有什么关系呢?
以 user 对 item 的评分预测问题为例,基于矩阵分解的协同过滤可以看成是FM的一个特殊例子。
在协同过滤中,对于每一个样本,FM可以将其看作特征只有 userid 和 itemid。
但是在实际FM中,我们的每个样本,可以有除了 userid, itemid 之外的很多特征组合而成。能够学到更多的组合模式。
2、 FM和神经网络
神经网络天然地难以直接处理高维稀疏的离散特征,因为这将导致神经元的连接参数太多。但是低维嵌入(embedding)技巧可以解决这个问题,词的分布式表达就是一个很好的例子。事实上 FM就可以看做对高维稀疏的离散特征做 embedding。
上面举的例子其实也可以看做将每一个 user 和每一个 item 嵌入到一个低维连续的 embedding 空间中,然后在这个 embedding 空间中比较 user 和 item 的相似性来学习 user 对 item 的偏好。
这跟 word2vec$^{[8]}$词向量学习类似,word2vec 将词 embedding 到一个低维连续空间,词的相似性通过两个词向量的相似性来度量。神经网络对稀疏离散特征做 embedding 后,可以做更复杂的非线性变换,具有比FM更大的潜力学习到更深层的非线性关系!基于这个思想,2016年,Google提出 wide and deep 模型用作 Google Play的app推荐$^{[9]}$它利用神经网络做离散特征和连续特征之间的交叉,神经网络的输出和人工组合较低维度的离散特征一起预测,并且采用端到端的学习,联合优化DNN和LR。如图所示,Catergorial 特征 embedding 到低维连续空间,并和连续特征拼接,构成了1200维的向量,作为神经网络的输入,神经网络采用三隐层结构,激活函数都是采用 ReLU,最后一层神经元的输出$a^{(lf)}$和离散特征$X$及人工叉积变换后的特征$\phi(\mathbf{x})$,一起预测
$$P(Y=1|\mathbf{x}) = \sigma\left(\mathbf{w}{wide}^T[\mathbf{x}; \phi(\mathbf{x})] + \mathbf{w}{deep}^T a^{(lf)} + b \right)$$
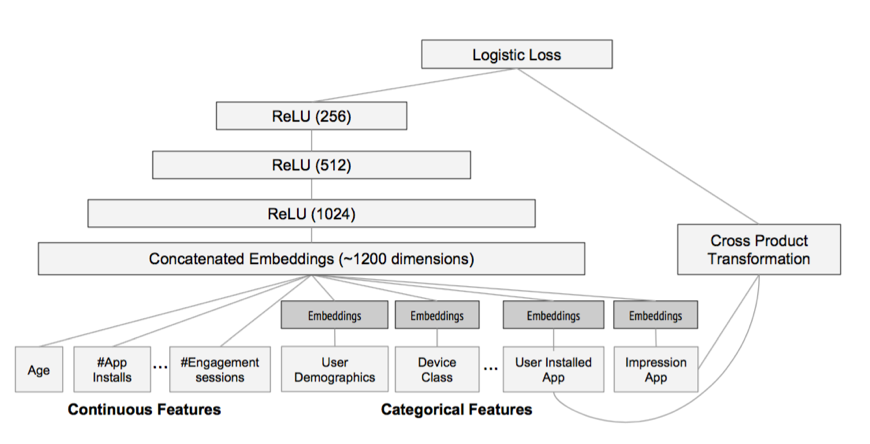
注意到,在 wide and deep 模型中,wide 部分是通过对用户安装过的 APP id 和用户 Impression App id 做叉积变换,解决 embedding 的过泛化问题。 所谓的过泛化,实际上是因为用户的偏好本身就很集中,即使相似的一些 item,用户也只偏好其中一部分,使得 query-item 矩阵稀疏但是高秩。 而这些信息实际上已经反映在用户已有的行为当中了,因此可以利用这部分信息,单独建立wide部分,解决deep部分的过泛化。
从另一个角度来看,wide 和 deep 部分分别在学习不同阶的特征交叉,deep 部分学到高阶交叉,而 wide 部分学到的是二阶交叉。 后来,有人用FM替换了这里wide部分的二阶交叉,使得模型对高度稀疏的特征的建模更加有效,因为高度稀疏特征简单的叉积变换也难以有效地学到二阶交叉, 这在前面已经叙述过了。因此,很自然的想法就是,用FM替换这里的二阶交叉,得到DeepFM模型$^{[10]}$
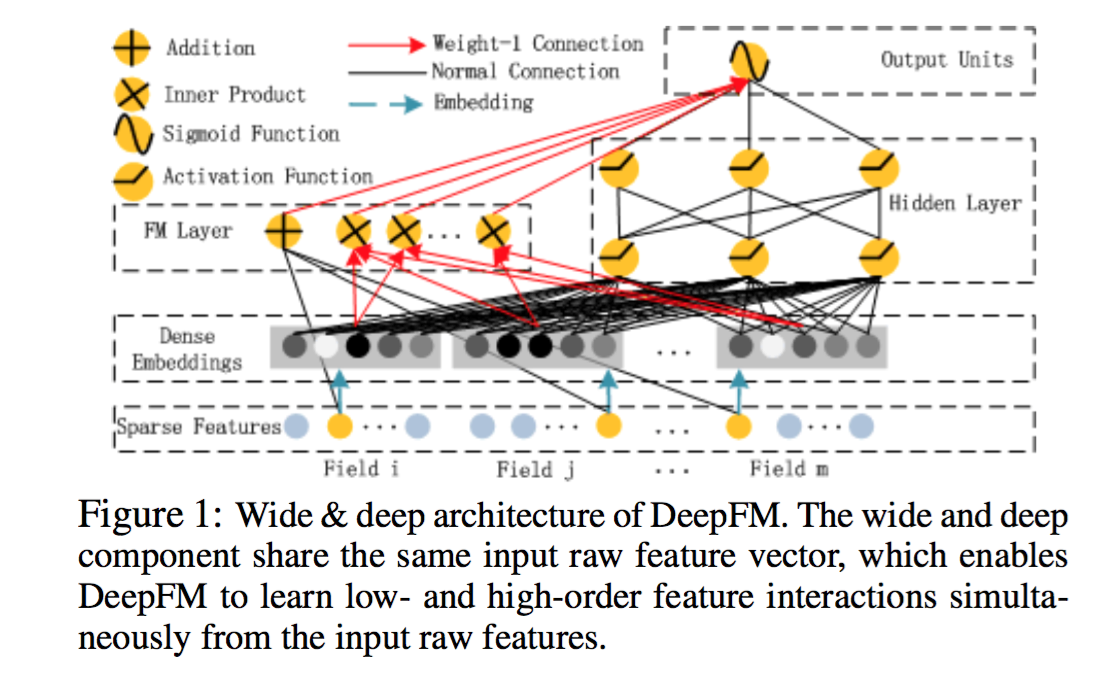
事实上,对于连续特征和非高度稀疏特征的高阶交叉,决策树似乎更加擅长。因此,很自然的想法是将GBDT也加到模型中。 但是问题是,决策树的优化方法和神经网络之类的不兼容,因此无法直接端到端学习。一种解决方案是,利用Boost融合的方案, 将神经网络、FM、LR当做一个模型,先训练一个初步模型,然后在残差方向上建立GBDT模型,实现融合。 微软的一篇文献$^{[10]}$也证实,Boost方式融合DNN和GBDT方案相比其他融合方案更优,因此这也不失为一种可行的探索方向!
如何实现因子分解机?
在我们动手写代码之前,我们先考虑API,我们需要哪里API,才能构成一个完整的Factorization Machine呢?
FM主要处理以下三种问题:
回归问题(Regression)
二分类问题(Binary Classification)
排序(Ranking)
这里,我们主要介绍二分类问题。
二分类问题的loss function为:
$$loss(\hat y , y) = \sum_{i=1}^m-ln \sigma{(\hat y , y)}$$
其中
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
使用基于随机梯度的方式求解:
我们可以设计API如下:
loadDataSet(data):
'''导入训练数据
input: data(string)训练数据
output: dataMat(list)特征
labelMat(list)标签
'''
sigmoid(inx):
''' sigmoid 函数
'''
initialize_v(n, k):
'''初始化交叉项
input: n(int)特征的个数
k(int)FM模型的超参数
output: v(mat):交叉项的系数权重
'''
stocGradAscent(dataMatrix, classLabels, k, max_iter, alpha):
'''利用随机梯度下降法训练FM模型
input: dataMatrix(mat)特征
classLabels(mat)标签
k(int)v的维数
max_iter(int)最大迭代次数
alpha(float)学习率
output: w0(float),w(mat),v(mat):权重
'''
getCost(predict, classLabels):
'''计算预测准确性
input: predict(list)预测值
classLabels(list)标签
output: error(float)计算损失函数的值
'''
getPrediction(dataMatrix, w0, w, v):
'''得到预测值
input: dataMatrix(mat)特征
w(int)常数项权重
w0(int)一次项权重
v(float)交叉项权重
output: result(list)预测的结果
'''
getAccuracy(predict, classLabels):
'''计算预测准确性
input: predict(list)预测值
classLabels(list)标签
output: float(error) / allItem(float)错误率
'''
1 |
|
———- 1.load data ———
———- 2.learning ———
——- iter: 0 , cost: 158.937545578
——- iter: 1000 , cost: 111.918235669
——- iter: 2000 , cost: 108.236920062
——- iter: 3000 , cost: 106.763275985
——- iter: 4000 , cost: 105.815190198
——- iter: 5000 , cost: 105.116731734
——- iter: 6000 , cost: 104.581618271
——- iter: 7000 , cost: 104.161136945
——- iter: 8000 , cost: 103.822237844
——- iter: 9000 , cost: 103.542542809
———-training accuracy: 0.990000
参考文献
[1] http://www.algo.uni-konstanz.de/members/rendle/pdf/Rendle2010FM.pdf
[2] http://www.cs.cmu.edu/~wcohen/10-605/2015-guest-lecture/FM.pdf
[3] http://www.algo.uni-konstanz.de/members/rendle/pdf/Rendle2010FM.pdf
[4] Koren Y, Bell R M, Volinsky C, et al. Matrix Factorization Techniques for Recommender Systems[J]. IEEE Computer, 2009, 42(8): 30-37.
[5] https://tracholar.github.io/machine-learning/2017/03/10/factorization-machine.html#fm与矩阵分解
[6] http://www.cnblogs.com/pinard/p/6370127.html
[7] https://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html
[8] Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]. neural information processing systems, 2013: 3111-3119.
[9] Guo H, Tang R, Ye Y, et al. DeepFM: A Factorization-Machine based Neural Network for CTR Prediction[J]. arXiv preprint arXiv:1703.04247, 2017.
[10] Ling X, Deng W, Gu C, et al. Model Ensemble for Click Prediction in Bing Search Ads[C]//Proceedings of the 26th International Conference on World Wide Web Companion. International World Wide Web Conferences Steering Committee, 2017: 689-698.
[11] http://blog.csdn.net/google19890102/article/details/45532745