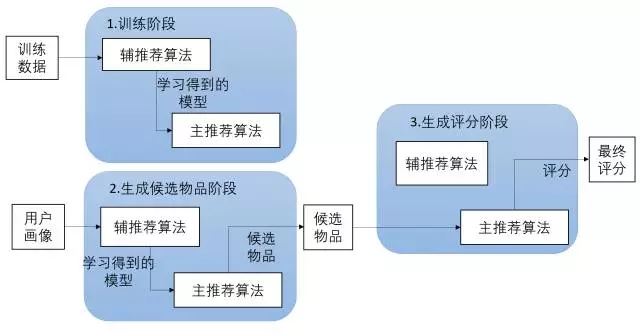
对传统推荐方法的一个小结,文章长度较长,分为两部分。
推荐系统的结构(Structure)
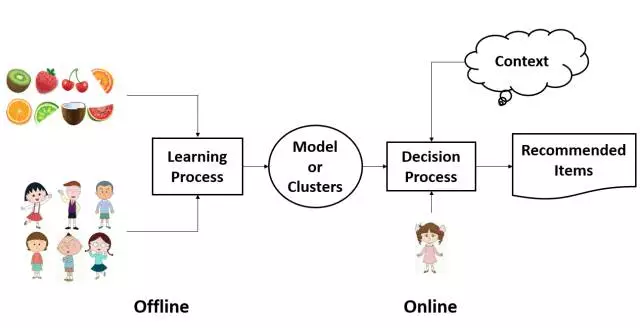
推荐引擎算法(Algorithm)
1、协同过滤推荐算法
1.1、关系矩阵与矩阵计算
在一个推荐系统中,存在三类关系:用户与用户(U-U矩阵)、物品与物品(I-I矩阵)和用户与物品(U-I矩阵)。
1.1.1、U-U矩阵
原理解读:
在基于用户相似度的协同过滤中,用户相似度的计算是基本前提。简单的方法可以采用余弦相似度,计算公式为:
$$similarity _ user _ value(i, j) = \frac{\sum_{c\in I_{ij}} (r_{i,c} - \bar{r_i}) (r_{j,c} - \bar{r_j}) }{ \sqrt{\sum_{c\in I_i} (r_{i,c} - \bar{r_i}) ^ 2} \sqrt{\sum_{c\in I_j} (r_{j,c} - \bar{r_j}) ^ 2} }$$
公式解答:
$I_{ij}$ 表示 用户 $i$ 和 用户 $j$ 共同评价过的 物品 的集合, $c$ 是这个集合中的某个 物品 , $r_{i,c}$ 表示 用户 $i$ 对 物品 $c$ 的评分, $r_{j,c}$ 表示 用户 $j$ 对 物品 $c$ 的评分, $\bar{r_i}$ 和 $\bar{r_j}$ 表示 用户 $i$ 和 用户 $j$ 对 该 物品 集合的平均评分。
实际操作:
input: 用户行为日志
output: 基于协同的用户相似度矩阵(也就是 user-user 矩阵)
A:从用户行为日志中获取用户与物品之间的关系数据,即用户对物品的评分数据。
B:对于 $n$ 个用户,依次计算用户 $1$ 与其他 $n-1$ 个用户的相似度;再计算用户 $2$ 与其他 $n-2$ 个用户的相似度。对于其中任意两个用户 $i$ 和 $j$ :
a) 查找两个用户共同评价过的物品集 $I_{ij}$ ;
b) 分别计算用户 $i$ 和 $j$ 对物品 的平均评分 $\bar{r_i}$ 和 $\bar{r_j}$ ;
c) 计算用户间相似度,得到用户 $i$ 和 $j$ 的相似度。
C. 将计算得到的相似度结果存储于数据库中。
1.1.2、I-I矩阵
原理解读:
在基于物品相似度的协同过滤中,物品相似度的计算是基本前提。将n个用户,看成物品的n个属性,简单的方法可以采用余弦相似度,计算公式为:
$$similarity _ itme_value(x_i, x_j) = \frac{\sum_{u\in U_{x_i, x_j}} (r_{u,x_i} - \bar{r_{x_i}}) (r_{u,x_j} - \bar{r_{x_j}}) }{ \sqrt{\sum_{u\in U_{x_i, x_j}} (r_{u,x_i} - \bar{r_{x_i}}) ^ 2} \sqrt{\sum_{u\in U_{x_i, x_j}} (r_{u,x_j} - \bar{r_{x_j}}) ^ 2} }$$
公式解答:
$U_{x_i, x_j}$表示 对物品 $x_i$ 和物品 $x_j$ 都做出过评价的用户的集合, $u$ 是这个集合中的某个用户 , $r_{u,x_i}$ 表示 用户 $u$ 对 物品 $x_i$ 的评分, $r_{u,x_j}$ 表示 用户 $u$ 对 物品 $x_j$ 的评分, $\bar{r_{x_i}}$ 和 $\bar{r_{x_j}}$ 分别表示 用户对物品$x_i$ 和 $x_j$的平均评分
实际操作:
input: 用户行为日志
output: 基于协同的物品相似度矩阵(也就是 item-item 矩阵)
A:从用户行为日志中获取用户与物品之间的关系数据,即用户对物品的评分数据。
B:对于 $n$ 个物品,依次计算物品 $1 $ 与其他 $n-1$ 个物品的相似度;再计算物品 $2$ 与其他 $n-2$ 个物品的相似度。对于其中任意两个物品 $i$ 和 $j$ :
a) 查找对物品 $i$ 和 $j$ 都做出过评价的用户集 $U_{ij}$ ;
b) 分别计算用户 对物品 $i$ 和 $j$ 的平均评分 $\bar{r_i}$ 和 $\bar{r_j}$ ;
c) 计算物品间相似度,得到物品 $i$ 和 $j$ 的相似度。
C. 将计算得到的相似度结果存储于数据库中。
1.1.3、U-I矩阵
在真实的推荐系统中,一方面U-I矩阵的行列数会随着用户和物品数量变得庞大,另一方面,因为用户实际上只能对有限数量的物品做出评价,所以U-I矩阵的内部会非常稀疏。系统在直接处理这些庞大稀疏矩阵时,耗费的时间、内存和计算资源都十分巨大。因此需要采取降低计算复杂度的方法。矩阵分解(matrix factorization)是一种有效降低矩阵计算复杂的方法,它的实质是将高维矩阵进行有效降维。
奇异值分解(SVD)
SVD将给定矩阵分解为3个矩阵的乘积:
$$M = U \Sigma V^T$$
式中,矩阵 $\Sigma$ 为对角阵,其对角线上的值 $\sigma$ 为矩阵M的奇异值。
按大小排列,代表着矩阵M的重要特征。将SVD用在推荐系统上,其意义是将一个稀疏性较高的评分矩阵 $M$ 分解为表示用户特性的 $U$ 矩阵,表示物品特性的 $V$ 矩阵,以及表示用户和物品相关性的矩阵$\Sigma$。
主成分分析(PCA)
在推荐系统中,对于有较多属性的物品(物品的信息用向量 $m[i_1, i_2, …, i_n]$ 表示)可用PCA来进行降维处理,将 $m \times n$的物品矩阵转化为$m \times k$的新矩阵。
1.2、基于记忆的协同过滤算法(memory-based)
1.2.1、基于用户的协同过滤算法
基于用户的协同过滤(user-based collaborative filtering)算法是推荐系统中最古老的算法,产生于1992年,最初应用于邮件过滤系统,1994年被GroupLens用于新闻过滤。在此之后直到2000年,该算法都是推荐系统领域最著名的算法。
原理解读:
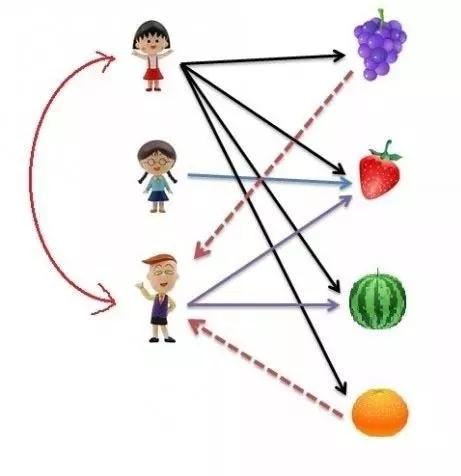
什么是基于用户的协同过滤算法?举个简单的例子,我们知道樱桃小丸子喜欢葡萄、草莓、西瓜和橘子,而我们通过某种方法了解到小丸子和花伦有相似的喜好,所以我们会把小丸子喜欢的而花伦还未选择的水果(葡萄和橘子)推荐给花伦。
通过上面的例子我们假设用户为$U_i(i = 1, 2, 3, …, n)$,物品$I_j(j=1, 2, 3, … n)$,$U_i$对$I_j$的评分为$r_{ij}$。
那么,基于用户的协同过滤算法(user-CF)主要包含以下两个步骤:
A: 搜集用户和物品的历史信息,计算用户$u_i$和其他用户的相似度$Sim(u_i, N_i)$,找到和目标用户$u_i$兴趣相似的用户集合$N(u_i)$
B: 找到这个集合$N(u_i)$中用户喜欢,且目标用户$u_i$还没消费过的商品,推荐给目标用户$u_i$
在上面的B步骤中,我们得到的物品集合可能包含很多物品,我们称呼这个物品集为候选物品集合,我们不可能将这么多物品同时推荐给用户,所以,我们在基于用户的协同过滤子引擎上,通过下面的公式来计算用户对物品的喜好程度:
$$p_{uj} = \frac{\sum\limits_{N_i \in N(u)} Sim(u, N_i) \times r_{N_{i,j}}}{\sum\limits_{N_i \in N(u)} Sim(u, N_i)}$$
上式中,$u$ 是我们的目标用户, $p_{uj}$ 表示的是用户 $u$ 对物品 $j$ 的喜好程度, $r_{N_i,j}$表示用户 $N_i$ 对物品 $j$ 的评分, $Sim(u, N_i)$ 表示用户 $u$ 和用户 $N_i$ 的相似度。
最后,根据 $p_{uj}$来对候选物品进行排序,来为用户推荐分值最高的 Top-N 个物品
实际操作:
input:用户行为日志,基于协同的用户相似性矩阵。
output:初始推荐结果
A. 访问用户行为日志,获取一段时间内的用户集合$U$。
B. 针对集合 $U$ 中每个用户 $u$:
a) 访问用户相似矩阵,获取与用户相似的用户合集$N(u)$。
b) 对于$N(u)$中的每一个用户$u_i$:
获取与用户$u_i$有关联的物品合集$I_{u_i}$。
针对物品合集$I_{u_i}$中的每个物品,计算用户的喜好程度。
c) 对集$I_{u_i}$中的所有物品按照用户偏好进行加权、去重、排序。
d) 取Top-N个物品,为每个物品赋予解释。
e) 保存Top-N个物品到初始推荐列表中。
适用性:
由于需计算用户相似度矩阵,基于用户的协同过滤算法适用于用户较少的场合; 由于时效性较强,该方法适用于用户个性化兴趣不太明显的领域。
1.2.2、基于物品的协同过滤算法
基于物品的协同过滤(item-based collaborative filtering)算法是目前业界应用最多的算法。无论是亚马逊网,还是Netflix、Hulu、Youtube,其推荐算法的基础都是该算法。
原理解读:
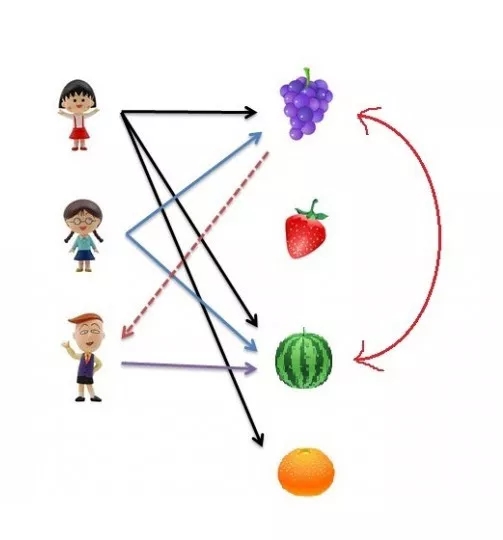
基于物品的协同过滤算法给用户推荐那些和他们之前喜欢的物品相似的物品。比如,我们知道樱桃小丸子和小玉都喜欢葡萄和西瓜,那么我们就认为葡萄和西瓜有较高的相似度,在花伦选择了西瓜的情况下,我们会把葡萄推荐给花伦。
Item-CF算法并不利用物品的内容属性计算物品之间的相似度,它主要通过分析用户的行为记录计算物品之间的相似度。该算法认为,物品A和物品B具有很大的相似度是因为喜欢物品A的用户大都也喜欢物品B。 补充一下:基于物品的协同过滤算法可以利用用户的历史行为给推荐结果提供解释比如给用户推荐《天龙八部》的解释可以是因为用户之前喜欢《射雕英雄传》
假设用户为$U_i(i =1, 2, 3, …, n)$,物品$I_j(j =1, 2, 3, …, n)$,$U_i$ 对 $I_j$ 的评分为$r_{i, j}$,基于物品的协同过滤算法主要分为两步:
A. 对于目标用户 $U_i$ 及其待评分的物品 $I_j$ ,根据用户对物品的历史偏好数据,计算物品 $I_j$ 与其他已评分物品之间的相似度 $Sim(j,i)$ ,找到与物品 $I_j$ 相似的物品合集 $N(I_j)$ ;
B. 根据用户对物品合集 $N(I_j)$ 的喜欢程度,选出 $N(I_j)$ 中目标用户可能喜欢的且没有观看过的推荐给目标用户并预测评分。
ItemCF通过下面的公式来计算用户对物品的喜好程度:
$$p_{ui} = \frac{\sum\limits_{ i \in N(I_j)} Sim(i, j) \times r_{uj}}{\sum\limits_{i \in N(I_j)} Sim(i, j)}$$
式中, $p_{ui}$ 表示用户 $u$ 对物品 $i$ 的喜欢程度,物品 $j$ 是用户买过的, $r_{uj}$ 表示用户 $u$ 对物品 $j$ 的评分。然后根据$p_{ui}$来对候选物品进行排序,为用户推荐分值最高的物品。
实际操作:
input:用户行为日志,基于协同的物品相似性矩阵
output:初始推荐结果
A. 访问用户行为日志,获取最近浏览过物品的用户集合U。
B. 针对集合U中每个用户u:
a) 选择用户当前正在浏览的商品 $i$
b) 访问物品相似矩阵,获取与 $i$ 相似的物品合集 $N(i)$
c) 计算用户对当前物品合集的喜好程度,并进行排序
d) 取Top-N个物品,为每个物品赋予解释。
e) 保存Top-N个物品到初始推荐列表中。
适用性
适用于物品数明显小于用户数的场合; 长尾物品丰富,用户个性化需求强烈的领域。

1.3、基于模型的协同过滤算法(model-based)
1.3.1、基于隐因子模型的推荐算法
隐语义模型是最近几年推荐系统领域最为热门的研究话题,它的核心思想是通过隐含特征(latent factor)联系用户兴趣和物品。也就是,对于某个用户,首先找到他的兴趣分类,然后从分类中挑选他可能喜欢的物品。
基本算法
基于兴趣分类的方法大概需要解决3个问题:
A. 如何给物品进行分类?
B. 如何确定用户对哪些类的物品感兴趣,以及感兴趣的程度?
C. 对于一个给定的类,选择哪些属于这个类的物品推荐给用户,以及如何确定这些物品在一个类中的权重?
隐含语义分析技术采取基于用户行为统计的自动聚类,可以自动解决物品分类问题。隐语义模型(latent factor model) (LFM) 通过如下公式计算用户 $u$ 对物品 $i$ 的兴趣:
$$Preference(u,i) = r_{ui} = p_u^T q_i = \sum_{f=1}^F p_{u,k} q_{i,k}$$
这个公式中,$p_{u,k}$ 和 $q_{i,k}$ 是模型的参数,其中,$p_{u,k}$ 度量了用户 $u$ 的兴趣和第 $k$ 个隐类的关系,而 $q_{i,k}$ 度量了第 $k$ 个隐类和物品 $i$ 之间的关系。
要计算这两个参数,需要一个训练集,对于每个用户 $u$ ,训练集里都包含了用户 $u$ 喜欢的物品和不感兴趣的物品,通过学习这个数据集,就可以获得上面的模型参数。
1.3.2、LFM和基于邻域的方法的比较
理论基础
LFM具有比较好的理论基础,它是一种学习方法,通过优化一个设定的指标建立最优的模型。基于邻域的方法更多的是一种基于统计的方法,并没有学习过程。
离线计算的空间复杂度
基于邻域的方法需要维护一张离线的相关表。在离线计算相关表的过程中,如果用户/物品数很多,将会占据很大的内存。而LFM在建模过程中,可以很好地节省离线计算的内存。
离线计算的时间复杂度
在一般情况下,LFM的时间复杂度要稍微高于UserCF和ItemCF,这主要是因为该算法需要多次迭代。但总体上,这两种算法在时间复杂度上没有质的差别。
在线实时推荐
UserCF和ItemCF在线服务算法需要将相关表缓存在内存中,然后可以在线进行实时的预测。LFM在给用户生成推荐列表时,需要计算用户对所有物品的兴趣权重,然后排名,不太适合用于物品数非常庞大的系统,如果要用,我们也需要一个比较快的算法给用户先计算一个比较小的候选列表,然后再用LFM重新排名。另一方面,LFM在生成一个用户推荐列表时速度太慢,因此不能在线实时计算,而需要离线将所有用户的推荐结果事先计算好存储在数据库中。因此,LFM不能进行在线实时推荐,也就是说,当用户有了新的行为后,他的推荐列表不会发生变化。
推荐解释
ItemCF算法支持很好的推荐解释,它可以利用用户的历史行为解释推荐结果。但LFM无法提供这样的解释,它计算出的隐类虽然在语义上确实代表了一类兴趣和物品,却很难用自然语言描述并生成解释展现给用户。
1.4、基于内容(CB)的推荐算法(content-based)
1.4.1、基础CB推荐算法
算法背景
基础CB(content-based)推荐算法利用物品的基本信息和用户偏好内容的相似性进行物品推荐。通过分析用户已经浏览过的物品内容,生成用户的偏好内容,然后推荐与用户感兴趣的物品内容相似度高的其他物品。
比如,用户近期浏览过冯小刚导演的电影“非诚勿扰”,主演是葛优;那么如果用户没有看过“私人订制”,则可以推荐给用户。因为这两部电影的导演都是冯小刚,主演都有葛优。
计算公式为:
$$Sim(U_i, I_j) = \sum_k \lambda_k Sim(U_{ik}, I_{jk})$$
式中, $U_i$ 表示用户, $I_j$ 表示商品, $U_{ik}$ 表示用户 $U_i$ 的第 $k$ 个特征,$I_{jk}$ 表示商品 $I_j$ 的第 $k$ 个特征。
所以 $Sim(U_i, I_j)$ 表示的是用户 $U_i$ 和商品 $I_j$ 的相似度。其中 $\lambda_k$ 可以表示第 $k$ 个特征的权重。
算法流程
input:物品信息,用户行为日志。
output:初始推荐结果。
A. 使用特征表示物品:每个物品$\vec{I} = (I_1, I_2, … , I_m)$,其中$I_i$表示物品的特征属性;
B. 从用户行为日志中,获取该用户所浏览、收藏、评价、分享的物品集合$M$,根据物品集合$M$中物品的特征数据,可以学到用户的内容偏好,按照 $\vec{U} = (U_1, U_2, … , U_m)$的格式表示出用户。
C. 选取用户未消费过的商品用来求用户、商品的相似度,选择其中较高的。
D. 保存Top-K个物品到初始推荐结果中。
适用场景
适用于基础CB架构的搭建,尤其是对新上线物品会马上被推荐非常有效,被推荐的机会与老的物品是相同的。
缺陷
需要手动设置各个特征,前期数据量不大的时候可能还好,假如数据量很大,则会比较麻烦。
1.4.2、基于TF-IDF的CB推荐算法
假设一个场景是要给用户推荐新闻、书籍,我们已知用户阅读过的新闻、书籍,该如何给用户推荐新的新闻或者书籍呢?
对于这样的场景我们需要从文字当中提取关键信息,这时可以采用TF-IDF(Term Frequency-Inverse Document Frequency)。TF-IDF算法被公认为信息检索中最重要的发明,在搜索、文献分类和其他相关领域有广泛应用。
TF-IDF是自然语言处理领域中计算文档中词或短语的权值的方法,是词频(Term Frequency, TF)和逆转文档频率(Inverse Document Frequency, IDF)的乘积。TF指的是某一个给定的词语在该文件中出现的次数,这个数字通常会被正规化,以防止它偏向长的文件(同一个词语在长文件里可能会比段文件有更高的词频,而不管该词语重要与否)。IDF是一个词语普遍重要性的度量,某一特定词语的IDF,可以由总文件数目除以包含该词语的文件数目,再将得到的商取对数得到。
算法原理
TF-IDF算法基于这样一个假设:若一个词语在目标文档中出现的频率高而在其他文档中出现的频率低,那么这个词语就可以用来区分出目标文档。这个假设的主要信息有两点:
- 在本文档出现的频率高;
- 在其他文档出现的频率低。
因此,TF-IDF算法的计算可以分为词频(TF)和逆转文档频率(IDF)两部分,由TF和IDF的乘积来设置文档词语的权重。
假设文档集包含的文档数为 $N$,文档集中包含关键词 $k_i$ 的文档数为 $n_i$ , $f_{ij}$ 表示关键词 $k_i$ 在文档 $d_j$ 中出现的次数, $f_{dj}$ 表示文档 $d_j$ 中出现的词语总数, $k_i$ 在文档 $d_j$ 中的 $TF_{ij}$ 定义未:
$$TF_{ij} = \frac{ f_{ij} }{ f_{dj} }$$
这个数字通常会被正规化,以防止它偏向长的文件。
IDF衡量词语的普遍重要性。 $\frac{n_i}{N}$ 表示某一词语在整个文档中出现的频率, 由它计算的结果取对数得到关键词 $k_i$ 的逆文档频率 $IDF_i$ :
$$IDF_i = log \frac{N}{n_i + 1}$$
由TF和IDF计算词语的权重为
$$w_{ij} = TF_{ij} \cdot IDF_i = \frac{ f_{ij} }{ f_{dj} } \cdot log \frac{N}{n_i + 1}$$
举一个例子就是,我们现在有 100000 篇新闻, 包含关键词“科比”的新闻有100篇, 在新闻《科比退役——时代的终结》 里面,“科比” 出现了 60 次, 这篇新闻的词语总数是 2000,那么 “科比” 在新闻《科比退役——时代的终结》 中的 $TF$ 为:
$$TF_{科比, 《科比退役——时代的终结》} = \frac{60}{2000}$$
关键词“科比”的 $IDF_{科比}$为:
$$IDF_{科比} = log \frac{100000}{100 + 1}$$
我们取出 Item 中的关键词,可以用这些关键词代表这篇新闻,就得到了这个Item 的特征表示(其实也直接对新闻类的 Item 直接使用 word2vec)。
然后,我们表示用户,对于用户来说,它看过了的新闻,用喜欢和不喜欢进行标记,然后根据已有数据我们可以用如下公式表示用户:
$$profile = \frac{\sum_{i=1}^a x_1 + x_2 + … + x_a}{a} - \frac{\sum_{i=1}^b x_1 + x_2 + … + x_b}{b}$$
其中 $x$ 是用户喜欢的item, $a$ 是喜欢item的总数, $y$ 是用户不喜欢的item, $b$ 是不喜欢item的总数。
这样就表示出了用户。
算法流程
input:新闻内容,用户行为日志。
output:初始推荐结果。
A. 使用特征表示新闻:每个新闻都提取 $m$ 个关键字来表示新闻的特征属性,然后每篇新闻用一个长度为$n (n > m)$的向量表示;
B. 从用户行为日志中,获取该用户所浏览、收藏、评价、分享的新闻集合$M$,根据新闻集合$M$中物品的特征数据,可以学到用户的内容偏好,按照 $\vec{U} = (U_1, U_2, … , U_n)$的格式表示出用户。
C. 选取用户未看过的新闻来求用户、新闻的相似度,选择其中较高的。
D. 保存Top-K个物品到初始推荐结果中。
适用场景
可以使用当前的用户评价来构建用户的个人信息;由于过程简单解释性强,推荐的结果容易被人接受;对于新物品来没有任何用户评分的也可以推荐给用户。
缺陷
可分析的内容有限,且新颖度较差,新用户需要用户的偏好信息,无法解决冷启动问题。
1.4.3、基于KNN的CB推荐算法
算法背景
KNN(k-Nearest Neighbor)算法基于这样的假设:如果在特征空间中,一个样本的k个最邻近样本中的大多数样本属于某一个类别,则该样本也属于这个类别。
算法原理
KNN在CB推荐算法中的应用与在CF推荐算法中的应用极为相似,它们都是要首先找到与目标物品相似的且已经被用户 $u$ 评价过的 $k$ 个物品,然后根据用户 $u$ 对这 $k$ 个物品的评价来预测其目标物品的评价。
它们的差别在于,CF推荐算法中的KNN是根据用户对物品的评分来计算物品间相似度的,而CB推荐算法中KNN是根据物品画像来计算相似度的,所以对于后者来说,如何通过物品画像来计算物品间的相似度是算法中的关键步骤。相似度的计算可以使用余弦相似度或Pearson相关系数的计算方法。
算法流程
input:用户已评分物品,目标物品 $I_j$ 。
output:用户对目标物品 $r_j$ 的评分。
A. 采用余弦相似度公式计算相似度。
B. 选择最近邻。在用户 $u$ 评过分的所有物品中,找出 $k$ 个与目标物品 $j$ 相似度最高的物品,并用 $N(u,j)$ 来表示这 $k$ 个物品的集合。
C. 计算预测值。在第二步的基础上,可使用以下公式计算用户对目标物品的评分:
$$\hat{r}{u,j} = \frac{\sum{n \in N(u,j)} S_{j,n} r_{u,n}}{ \sum_{n \in N(u,j)} S_{j,n} }$$
式中, $\hat{r}{u,j}$ 表示用 $u$ 对物品 $j$ 的预测评分, $S{j,n}$ 是物品相似度, $r_{u,n}$ 表示用户对物品 $n$ 的评分。
1.4.4、基于Rocchio的CB推荐算法
算法背景
Rocchio是从用户浏览历史中抽取用户喜好的物品特征来构建用户画像的一种常用算法,是信息检索领域处理相关反馈(Relevance Feedback)的一个著名算法。它提供了如何通过用户浏览的物品,反馈计算用户特征向量中属性值的方法。
举个简单例子,假如用户观看过“星球大战”和“加勒比海盗”,并给予高分,那么根据用户的行为历史数据构建画像时,用户的特征向量可表示为{“动作”:1,“欧美”:1,“科幻”:1,“冒险”:0.5}。
算法原理
Rocchio算法基于这样的假设:如果我们需要计算出最精准度的用户特征向量 $U_c$ ,那么这个用户特征向量应该与用户喜欢的物品特征最相似,与用户讨厌的物品特征最不同。若 $V_l$ 表示用户喜欢的物品, $V_h$ 表示用户讨厌的物品,那么根据Rocchio算法的思想,定义最优的用户特征向量为:
$$U_{opt} = arg max [Sim(U_c, V_l) - Sim(U_c, V_h)]$$
更新用户的特征向量,修改公式为:
$$U_{opt} = \alpha U_0 + \beta \frac{1}{ |V_l| } \sum_{\vec{w}_j \in V_l} \vec{w}_j - \gamma \frac{1}{ |V_h| } \sum_{\vec{w}_j \in V_h} \vec{w}_j$$
式中, $U_0$ 是原始的用户特征向量,$\alpha$、$\beta$、$\gamma$ 为权重。若用户新的历史数据较多,那么可以增大 $\beta$ 和 $\gamma$ 的值,反之,用户更新数据较少则可以适当减小$\beta$ 和 $\gamma$ 的值。
在基于内容的物品推荐中,根据用户的历史行为数据建立用户画像,我们可以采用Rocchio算法不断地调整用户的特征向量 $U_c$ 。
1.4.5、基于决策树的CB推荐算法
算法背景
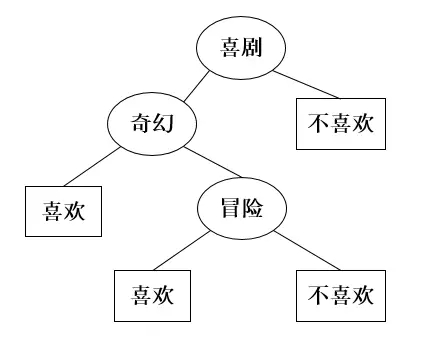
基于决策树的推荐算法在训练阶段会生成一个显示的决策模型。决策树可以通过训练数据构建并有效判断一个新的物品是否可能受到欢迎。当物品的特征属性较少时,采用决策树算法能够取得不错的效果,另外,决策树学习的思想也比较容易被理解,在物品推荐时的可解释性较好。
算法原理
在物品推荐系统中,决策树的内部节点通常表示物品的特征属性,这些节点用于区分物品集合,例如,通过物品中是否包含这个特征将其进行分类。在只有两个分类的简单数据集中,用户是否对物品感兴趣一般出现在决策树的叶子节点上。
1.4.6、基于线性分类的CB推荐算法
算法背景
将基于内容的物品推荐问题视为分类问题时,可以采用多种机器学习方法。从一个更抽象的角度上看,大部分学习方法致力于找到一个可以准确区分用户喜欢和不喜欢的物品的线性分类模型系数。
将物品数据用 $n$ 维特征向量来表示,线性分类器试图在给定的物品特征空间中找到一个能够将物品正确分类的平面,一类点尽可能在平面的某一边(喜欢),另一类在平面的另一边(不喜欢)。
算法原理
基于线性分类器的CB推荐算法通过物品特征的线性组合进行分类。若输入的物品特征向量为 $\vec{v} = (v_1, v_2, … , v_n)$ ,输出的结果 $y$ 表示用户是否喜欢物品,则线性分类器可以表示为:
$$y = \vec{w}^T \cdot \vec{v} = \sum_{i=1}^n \vec{w}_i \cdot \vec{v}_i $$
式中, $\vec{w}_i$ 表示物品特征向量对应的权重,根据输入的物品特征属性做出决定输出结果。
1.4.7、基于朴素贝叶斯的CB推荐算法
算法背景
基于朴素贝叶斯的推荐系统假设用户和物品的特征向量中的各个分量之间条件独立,判断用户是否对某个物品有兴趣的方法是将这个问题转化为分类问题:喜欢和不喜欢。
计算物品分类情况的后验概率为:
$$P(C|v) = \frac{P(v|C) \times P(C)}{P(v)} = \frac{\prod_{i=1}^n (v_i|C) \times P(C)}{P(v)}$$
式中, $v_i(i=1, 2, 3, …, n)$ 表示物品的相关属性;$C$ 为物品的分类, $P(v_i | C=c)$ 表示在分类 $c$ 中一个物品的特征属性 $v_i$ 出现的概率。这样,物品分类的后验概率可以通过观察分析训练数据得到。
算法原理
推荐系统中,分类 $c$ 下的一个物品特征属性 $v_i$ 的条件概率用在分类 $c$ 下所有物品中出现的频率近似表示,即
$$P(v_i | C) = \frac{CountTerms(v_i, item(c))}{ALLterms(item(c))}$$
式中, $CountTerms(v_i, item(c))$ 表示在标记为的物品 $c$ 出现的次数, $ALLterms(item(c))$ 表示在这些物品中出现的所有特征属性的个数。为了预防计算概率为0的情况,对式子进行平滑,新公式如下:
$$\hat{P}(v_i | C) = \frac{CountTerms(v_i, item(c)) + 1}{ALLterms(item(c)) + |V|}$$
式中, $|V|$ 表示所有物品中的出现的不同特征属性数。
1.5、基于知识的推荐算法(knowledge-based)
1.5.1、概述
基于知识(Knowledge-based, KB)的推荐算法,是区别于基于CB和基于CF的常见推荐方法。
如果说CB和CF像通用搜索引擎的话,KB好比某个领域的垂直搜索引擎,可以提供该领域的特殊需求,包括专业性的优质特征,帮助提高搜索引擎在特定领域的服务。
以视频推荐为例,一部电影的上映时期和档期热度,哪些导演执导的一定是大片,变形金刚和指环王系列口碑肯定不会太差,都是非常有价值的推荐信息。此外,基于知识的推荐,也更容易满足主观个性化需求。例如,对于VIP用户,如果配置好了偏好,就可以为其提供更加精准的推荐服务。
1.5.2、约束知识与约束推荐算法(相当于线性规划)
如今网上购物所能涵盖的物品越来越丰富,人们逐渐发现推荐系统的CF和CB推荐算法并不能很好地适应某些特殊物品的推荐需求。例如,更新换代非常快的而人们又通常不会经常更换的电子产品。对于这些产品来说,其各方面的性能参数在几年间就会有很大变化,代表历史偏好的用户画像并不能很好地反映用户当前的购买需求,于是就需要推荐系统将用户当前的需求作为重要信息参考源。人们发现可以利用物品的参数特征等属性形成约束知识,再将用户对物品的特定刻画为约束条件,然后经过对物品集合的约束满足问题的求解,就可以得到用户所期望的物品了。
创建推荐任务
推荐任务是以元组 $(R,I)$ 的形式表示出来,其中用集合 $R$ 表示目标用户对物品的特定需求,即对物品的约束条件,用集合 $I$ 表示一个物品集合。推荐的任务就是从集合 $I$ 中确定出能够满足集合 $R$ 要求的物品集。
推荐任务的解决
推荐任务的解决是以找到可能的集合 $S$ 为目标,集合 $S$ 应满足的条件是 $S \subseteq I$ ,并且 $\forall I_i \in S : I_i \in \sigma_{(R)} I$ ,其中 $\sigma$ 表示对集合 $I$ 进行合取查询的运算符,$R$ 表示对物品的约束条件或选择标准。
冲突集
冲突集 $CS$ 应满足的条件为 $CS \subseteq R$ :,并且 $\sigma_{(CS)}I \neq \phi$ 。特别地,当不存在集合 $C’S’ \subset CS$ 时,集合 $CS$ 被称为最小冲突集。
诊断集
诊断集 $\Delta$ 应满足的条件是 $\Delta \subseteq R$ ,并且。特别地$\sigma_{(CS)}I \neq \phi$,当不存在集合$\Delta’ \subset \Delta$时,集合 $\Delta$ 被称为最小诊断集。
1.5.3、关联知识与关联推荐算法
算法原理
关联知识以关联规则为表现形式,用以描述数据库中数据之间关联性的知识。在推荐系统领域,可以通过对用户画像中关联规则的挖掘分析来分析用户的习惯,发现物品之间的关联性,并利用这种关联性指导系统做出推荐。
算法流程
input: $n$ 个用户画像。
output:针对目标用户 $u$ 的Top-N推荐列表。
A. 从系统中的$n$个用户画像中挖掘出所有的强关联规则,建立集合 $P_u$
以表示目标用户 $u$ 尚未观看但极有可能感兴趣的物品。
B. 再次使用置信度对集合 $P_u$ 中的物品进行高低排序。
C. 取出排序列表中的前 $N$ 个物品构成Top-N推荐列表。 由于对系统中全体用户的画像进行规则关联挖掘意义不明显且计算量大,所以基于关联规则的推荐算法常与CF推荐算法混合使用。在这类混合方案中,使用了CF推荐算法中的最近邻算法将用户画像数目 $n$ 限定在目标用户的最邻近范围内,使得关联规则挖掘算法处理的数据规模被有针对性地限定在一定范围内。
1.6、混合推荐算法 (Hybrid Recommendation)
各种推荐方法都有优缺点,为了扬长补短,在实际中常常采用混合推荐(Hybrid Recommendation)。
研究和应用最多的是内容推荐和协同过滤推荐的组合。最简单的做法就是分别用基于内容的方法和协同过滤推荐方法去产生一个推荐预测结果,然后用某方法组合其结果。
尽管从理论上有很多种推荐组合方法,但在某一具体问题中并不见得都有效,组合推荐一个最重要原则就是通过组合后要能避免或弥补各自推荐技术的弱点。
- 加权式:加权多种推荐技术结果。
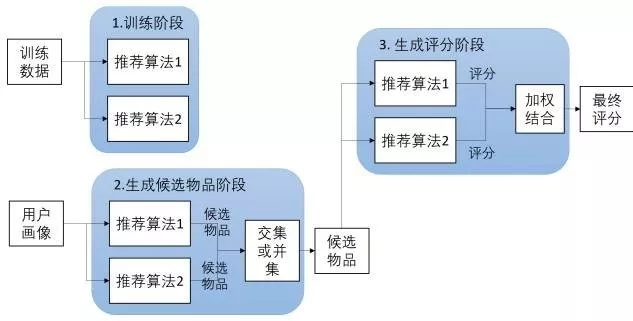
- 切换式:根据问题背景和实际情况或要求决定变换采用不同的推荐技术。
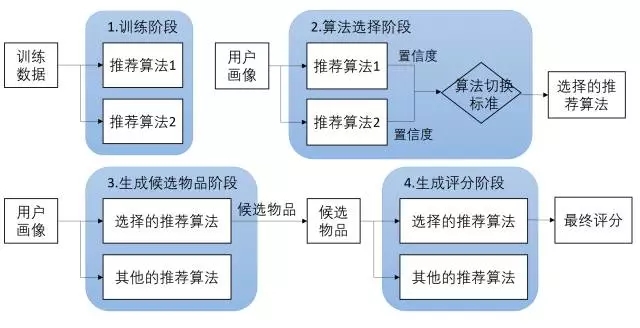
- 混杂式:同时采用多种推荐技术给出多种推荐结果为用户提供参考。
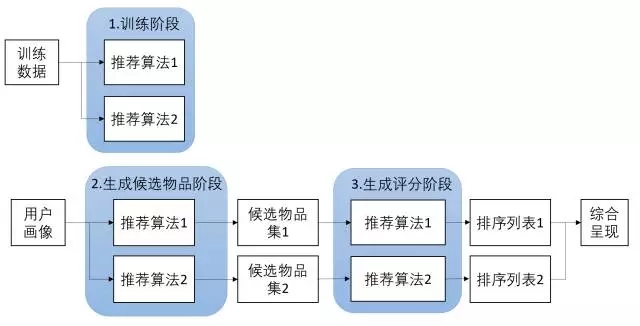
- 特征组合:组合来自不同推荐数据源的特征被另一种推荐算法所采用。
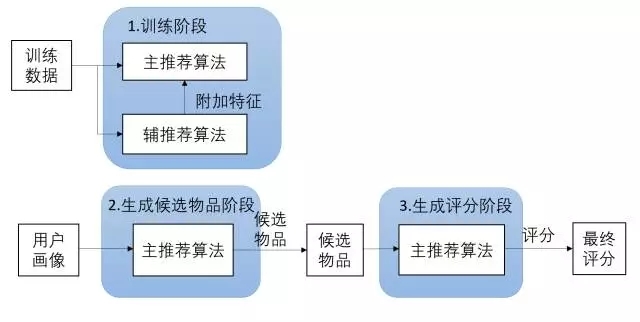
- 层叠式:先用一种推荐技术产生一种粗糙的推荐结果,第二种推荐技术在此推荐结果的基础上进一步作出更精确的推荐。
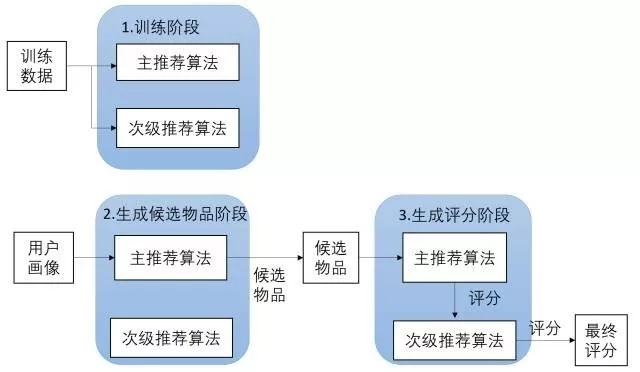
- 特征补充:一种技术产生附加的特征信息嵌入到另一种推荐技术的特征输入中。
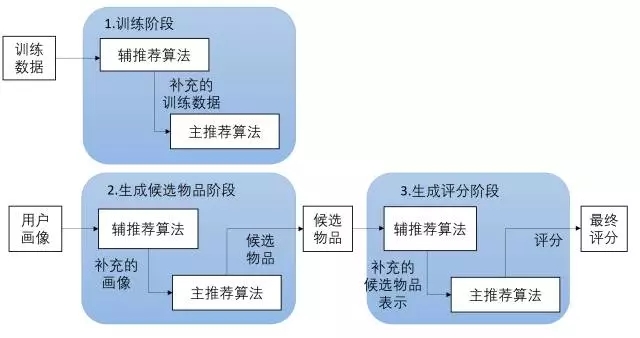
- 级联式:用一种推荐方法产生的模型作为另一种推荐方法的输入。