详细剖析RNN理论、变种和应用
一、RNN(循环神经网络)
1.1 RNN的原理
以前我们写过的 Network 的结果都是反馈给下一层。
那在RNN中,我们不仅要输出结果,还要输出一个隐含状态,给当前层在处理下一个样本时使用。
结构图如下所示:
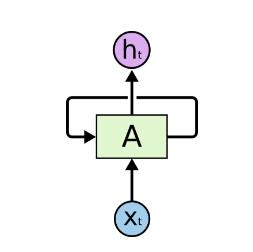
可以看到,跟普通的 Neural Network 相比,我们这里仅仅是多了一个隐含状态,那么这个多出来的隐含状态有什么好处呢?
这个隐含状态,我们可以看作是上一个样本遗留给我们的信息,通过这个信息,我们可以把握过去样本的特征,结合当前的样本,组成一种类似于 “时间序列” 样本信息,从而让模型有了处理前后有依赖关系数据样本的能力。
举个例子:
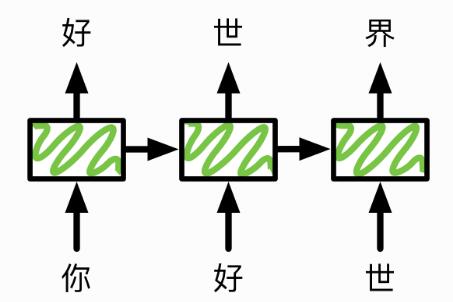
语言模型的任务是给定句子的前 $t$ 个字符,然后预测第 $t+1$ 个字符。假设我们的句子是“你好世界”,使用循环神经网络来预测的一个做法是,在时间 $1$ 输入“你”,预测“好”同时生成一个隐含状态;
在时间 $2$ 向同一个网络输入刚才生成的隐含状态 和 “好” 去预测“世”。同时输出一个更新过的隐含状态。
对于这个隐含状态, 我们会希望前面的信息能够保存在这个隐含状态里,从而提升预测效果。下图展示了这个过程。
1.2 RNN的公式表示
针对输入输出加上时间状态 $t$。在 $t$ 时刻,我们的输入为 $X_t$ 和 $H_{t-1}$,经过一个隐含层之后,我们有输出 $H_t$,经过最后的输出层得到 $\hat{Y_t}$。
其中 $X_t \in R^{n \times x}$ (样本数量为 $n$,每个样本特征向量维度是 $x$) ; $H_{t-1} \in R^{n \times h}$ (其中隐含层长度为 $h$)
隐含层的计算公式为:
$$\mathbf{H}_t = \phi(\mathbf{X}t \mathbf{W}{xh} + \mathbf{H}{t-1} \mathbf{W}{hh} + \mathbf{b}_h)$$
其中 $\mathbf{W}{xh}$ 和 $\mathbf{W}{hh}$ 是隐含层的权重, $\mathbf{b}_h$ 是隐含层的 bias。
输出层的计算公式为:
$$\hat{\mathbf{Y}}_t = \text{softmax}(\mathbf{H}t \mathbf{W}{hy} + \mathbf{b}_y)$$
其中 $\mathbf{W}_{hy}$ 是输出层权重,$\mathbf{b}_y$ 是输出层的 bias
最开始的隐含状态里的元素通常会被初始化为0,也就是 $H_0$ 是个零矩阵。
1.3 RNN的变种
1.3.1 one to many:
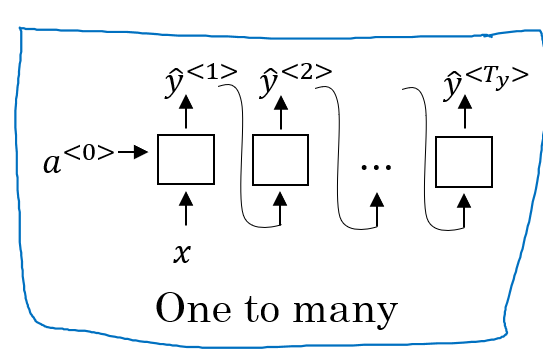
Music generation 、 poem generation: 我们给定起始的几个单词或者音符,自动为我们将剩下的内容补齐,从而创作出一首音乐或者一首诗词。这个时候,我们就可以 one to many 使用来解决这类问题。
1.3.2 many to one:
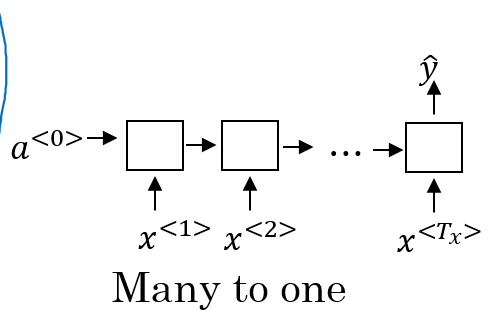
Setiment Classfication:比如,给定我们一个电影评论,我们来判断这个电影评论的情感好坏,用 1-5 的分数来表示用户对电影的喜好程度。 这个时候,我们就可以使用 many to one 来解决这类问题。
1.3.3 many to many with the same sequence:
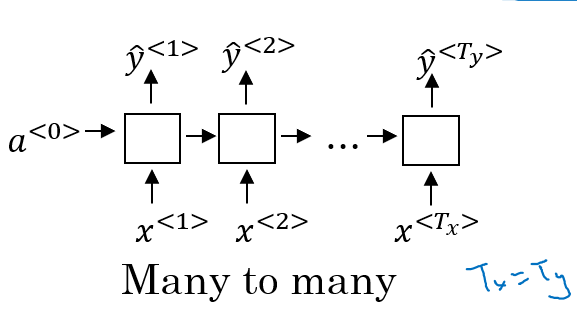
Name entity recognition: 给定我们一句话 Yesterday Harry Potter met Hermione Granger 我们判断其中的那些单词是姓名。 对应的输出应该是 0 1 1 0 1 1。这个时候,我们就可以使用 many to many with the same sequence 来解决这类问题。
1.3.4 many to many with the different length sequence (encoder-decoder)
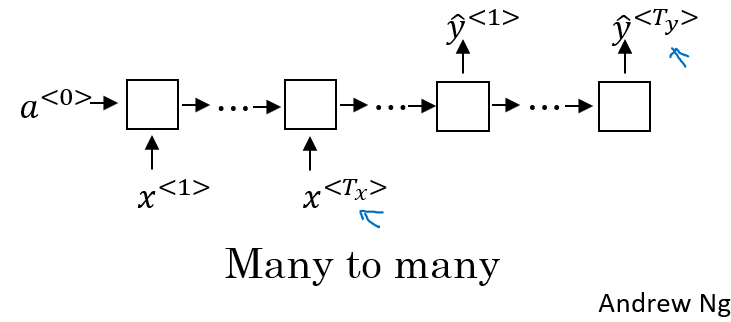
Machine translation:英语和中文的翻译,通常情况下,英语用十几个词表示的句子,中文几个词就够了。那么这个时候,我们就可以使用 encoder-decoder 来解决这类问题。
1.4 RNN的缺陷
1.4.1 时间反向传播(BPTT) 和 梯度爆炸(explosion) 和 梯度消失(valishing)
为什么会出现 explosion 或 valishing 呢?
我们需要先介绍循环神经网络中模型梯度的计算和存储,也即通过时间反向传播(back-propagation through time)简称 BPTT
事实上,所谓通过时间反向传播只是反向传播在循环神经网络的具体应用。我们只需将循环神经网络按时间展开,从而得到模型变量和参数之间的依赖关系,并依据链式法则应用反向传播计算梯度。
为了方便演示,我们先来看一个例子。
给定一个输入为 $\mathbf{x}_t \in \mathbb{R}^x$ (每个样本输入向量长度为 $x$) 和对应真实值为 $y_t \in \mathbb{R}$ 的时许数据训练样本($t = 1, 2, \ldots, T$ 为时刻),为了简单,我们不考虑偏差 $b$, 那么隐含层的表达式可以写成:
$$\mathbf{h}t = \phi(\mathbf{W}{hx} \mathbf{x}t + \mathbf{W}{hh} \mathbf{h}_{t-1})$$
$\mathbf{W}{hx} \in \mathbb{R}^{h \times x}$ 和 $\mathbf{W}{hh} \in \mathbb{R}^{h \times h}$ 是隐含层模型参数。
$\mathbf{h}_t \in \mathbb{R}^h$ 是 $t$ 时刻,向量长度为 $h$ 的隐含层变量,
同时,我们考虑相应时刻的输出层变量 $\mathbf{o}_t \in \mathbb{R}^y$ ,为了简单,我们不考虑偏差项。
$$\mathbf{o}t = \mathbf{W}{yh} \mathbf{h}_{t}$$
其中 $\mathbf{W}_{yh} \in \mathbb{R}^{y \times h}$ 表示输出层模型参数。
给定每个时刻损失函数计算公式 $\ell$ ,长度为 $T$ 的整个时序数据的损失函数 $L$ 定义为:
$$L = \frac{1}{T} \sum_{t=1}^T \ell (\mathbf{o}_t, y_t)$$
这也是模型最终需要被优化的目标函数。
为了可视化模型变量和参数之间在计算中的依赖关系,我们可以绘制计算图。我们以时序长度 $T=3$ 为例。
PS:图片来自 李沐gluon教程——通过时间反向传播
在上图中,模型的参数是$\mathbf{W}{hx}$、$\mathbf{W}{hh}$和$\mathbf{W}_{yh}$。为了在模型训练中学习这三个参数,以随机梯度下降为例,假设学习率为$η$,我们可以通过
$$\mathbf{W}{hx} = \mathbf{W}{hx} - \eta \frac{\partial L}{\partial \mathbf{W}_{hx}}$$
$$\mathbf{W}{hh} = \mathbf{W}{hh} - \eta \frac{\partial L}{\partial \mathbf{W}_{hh}}$$
$$\mathbf{W}{yh} = \mathbf{W}{yh} - \eta \frac{\partial L}{\partial \mathbf{W}_{yh}}$$
来不断迭代模型参数的值。因此我们需要模型参数梯度 $\partial L/\partial \mathbf{W}{hx}$、$\partial L/\partial \mathbf{W}{hh}$、$\partial L/\partial \mathbf{W}_{yh}$
为此,我们可以按照反向传播的次序依次计算并存储梯度。
为了表述方便,对输入输出 $\mathsf{X}, \mathsf{Y}, \mathsf{Z}$ 为任意形状张量的函数 $\mathsf{Y}=f(\mathsf{X})$ 和 $\mathsf{Z}=g(\mathsf{Y})$ ,我们使用
$$\frac{\partial \mathsf{Z}}{\partial \mathsf{X}} = \text{prod}(\frac{\partial \mathsf{Z}}{\partial \mathsf{Y}}, \frac{\partial \mathsf{Y}}{\partial \mathsf{X}})$$
来表达链式法则。
回到刚才的模型中,我们首先计算出目标函数有关各时刻输出层变量的梯度 $\partial L/\partial \mathbf{o}_t \in \mathbb{R}^y$ 可以很容易地计算
$$\frac{\partial L}{\partial \mathbf{o}_t} = \frac{\partial \ell (\mathbf{o}_t, y_t)}{T \cdot \partial \mathbf{o}_t}$$
事实上,这时我们已经可以计算目标函数有关模型参数 $\mathbf{W}{yh}$ 的梯度 $\partial L/\partial \mathbf{W}{yh} \in \mathbb{R}^{y \times h}$ 。需要注意的是,在计算图中,$\mathbf{W}_{yh}$ 可以经过 $\mathbf{o}_1, \ldots, \mathbf{o}_T$ 通向 $L$ ,依据链式法则,
$$\frac{\partial L}{\partial \mathbf{W}{yh}}= \sum{t=1}^T \text{prod}(\frac{\partial L}{\partial \mathbf{o}_t}, \frac{\partial \mathbf{o}t}{\partial \mathbf{W}{yh}})= \sum_{t=1}^T \frac{\partial L}{\partial \mathbf{o}_t} \mathbf{h}_t^\top$$
其次,我们注意到隐含层变量之间也有依赖关系。 对于最终时刻 $T$ , 在计算图中, 隐含层变量 $\mathbf{h}_T$ 只经过 $\mathbf{o}_T$ 通向 $L$。因此我们先计算目标函数有关最终时刻隐含层变量的梯度 $\partial L/\partial \mathbf{h}_T \in \mathbb{R}^h$ 。依据链式法则,我们得到
$$\frac{\partial L}{\partial \mathbf{h}_T} = \text{prod}(\frac{\partial L}{\partial \mathbf{o}_T}, \frac{\partial \mathbf{o}_T}{\partial \mathbf{h}T} ) = \mathbf{W}{yh}^\top \frac{\partial L}{\partial \mathbf{o}_T}$$
为了简化计算,我们假设激活函数 $\phi(x) = x$ 。 接下来,对于时刻 $t < T$, 在计算图中, 由于 $\mathbf{h}t$ 可以经过 $\mathbf{h}{t+1}$ 和 $\mathbf{o}_t$ 通向 $L$ ,依据链式法则, 目标函数有关隐含层变量的梯度 $\partial L/\partial \mathbf{h}_t \in \mathbb{R}^h$ 需要按照时刻从晚到早依次计算:
$$\frac{\partial L}{\partial \mathbf{h}t} = \text{prod}(\frac{\partial L}{\partial \mathbf{h}{t+1}}, \frac{\partial \mathbf{h}_{t+1}}{\partial \mathbf{h}_t} ) + \text{prod}(\frac{\partial L}{\partial \mathbf{o}_t}, \frac{\partial \mathbf{o}_t}{\partial \mathbf{h}t} ) = \mathbf{W}{hh}^\top \frac{\partial L}{\partial \mathbf{h}{t+1}} + \mathbf{W}{yh}^\top \frac{\partial L}{\partial \mathbf{o}_t}$$
将递归公式展开,对任意$1 \leq t \leq T$,我们可以得到目标函数有关隐含层变量梯度的通项公式
$$\frac{\partial L}{\partial \mathbf{h}t} = \sum{i=t}^T {(\mathbf{W}{hh}^\top)}^{T-i} \mathbf{W}{yh}^\top \frac{\partial L}{\partial \mathbf{o}_{T+t-i}}$$
由此可见,当每个时序训练数据样本的时序长度 $T$ 较大或者时刻 $t$ 较小,目标函数有关隐含层变量梯度较容易出现 衰减(valishing)和 爆炸(explosion)。想象一下$2^{30}$和$0.5^{30}$会有多大。
有了各时刻隐含层变量的梯度之后,我们可以计算隐含层中模型参数的梯度 $\partial L/\partial \mathbf{W}{hx} \in \mathbb{R}^{h \times x}$ 和 $\partial L/\partial \mathbf{W}{hh} \in \mathbb{R}^{h \times h}$ 。在计算图中,它们都可以经过 $\mathbf{h}_1, \ldots, \mathbf{h}_T$ 通向$L$。依据链式法则,我们有
$$\frac{\partial L}{\partial \mathbf{W}{hx}} = \sum{t=1}^T \text{prod}(\frac{\partial L}{\partial \mathbf{h}_t}, \frac{\partial \mathbf{h}t}{\partial \mathbf{W}{hx}}) = \sum_{t=1}^T \frac{\partial L}{\partial \mathbf{h}_t} \mathbf{x}_t^\top$$
$$\frac{\partial L}{\partial \mathbf{W}{hh}} = \sum{t=1}^T \text{prod}(\frac{\partial L}{\partial \mathbf{h}_t}, \frac{\partial \mathbf{h}t}{\partial \mathbf{W}{hh}}) = \sum_{t=1}^T \frac{\partial L}{\partial \mathbf{h}t} \mathbf{h}{t-1}^\top$$
1.4.2 只考虑到了前序信息,后序信息没有考虑
二、GRU
三、LSTM
四、参考
(2) 李沐gluon学习教程
(3) The Unreasonable Effectiveness of Recurrent Neural Networks
