edx 课程《Introduction to Probability - The Science of Uncertainty》Unit2 笔记
Unit2 Conditioning and independence
1. Conditioning and Bayes’ rule(条件概率和贝叶斯公式)
假设,我们现在在长沙市中随机选取一个人,这个人年龄低于18岁的概率,会是多少呢? 我们先猜测这个概率是 $25\%$ ,好的,那么接下来,我告诉你这个人结婚了,那么你猜测这个人年龄地狱18岁的概率又是多少呢?$5 \%$ 么?
想一下,在刚才的情形中,发生了什么导致我们猜测此人年龄小于18岁的概率一下子下降了这么多。
我们得到了一些额外的信息,这些额外的信息导致我们修正了猜测的概率。于是,这个被额外信息修正过的概率被我们称为 “条件概率”。
1.1 条件概率的定义
${\bf P}(A|B)$ 表示的是在事件 $B$ 发生的情况下,事件 $A$ 发生的概率是多少。
所以,条件概率的定义就是:
$$P(A|B) = \frac{P(A \cap B)}{P(B)}$$
注意,当且仅当P(B) > 0的时候,这个定义才有意义
举一个例子:
假设,我们现在有一个四面体的骰子(上面印有 1、2、3、4),现在,这个骰子连续投掷两次,分别用事件 $X$ 和事件 $Y$ 表示,所以可能结果一共有16种。
现在设事件 $B$ 表示的是 $min(X,Y) = 2$ 发生的情况。那么经过简单运算之后 $P(B) = \frac{5}{16}$
我们再设事件 $M = max(X,Y)$
现在,我们求 $P(M=1 | B)$ 的值。
在事件 $B$ 发生的情况下, $X$ 和 $Y$ 都应该大于或等于2 。那么显然, 不可能发生 $M=1$ 的情况,所以 $P(M=1 | B)=0$
那么 $P(M=3 | B)$呢?
根据条件可以知道 $P(M=3 \cap B) = \frac{2}{16}$ 且 $P(B) = \frac{5}{16}$ 于是由条件概率的定义可以得出 $P(M=1 | B) = /frac{2}{5}$
1.2 条件概率的性质
条件概率依旧是概率,所以可以从概率的性质那里进行推导
- $P(A|B) > 0$ 且 $P(B)>0$ 必须成立
- $P(\Omega | B) = \frac{P(\Omega \cap B)}{P(B)} = \frac{P(B)}{P(B)} = 1$
- $P(B | B) = \frac{P(B \cap B)}{P(B)} = \frac{P(B)}{P(B)} = 1$
- 如果 $A \cap C = \varnothing$ , 那么 $P(A \cup C | B) = P(A|B) + P(C|B)$
4.的证明如下所示:
$P(A \cup C | B) = \frac{P((A \cup B) \cap B)}{P(B)} = \frac{P((A \cap B) \cup (C \cap B))}{P(B)} = \frac{P((A \cap B) + (C \cap B))}{P(B)} = P(A|B) + P(C|B)$
1.3 条件概率例子
假设现在有一架飞机,它飞过某地区,该地区的雷达有检测功能,然后已知事件 $A$ 表示飞机飞过该地区,事件 $B$ 表示雷达发现了某个东西。
还知道如果飞机飞过、雷达能够检测出它是飞机的概率为 $P(B|A) = 0.99$ ,飞机没经过,但是雷达误检的概率 $P(B|A^c) = 0.1$ 且飞机飞过该区域 $P(A) = 0.05$
那么,雷达能够拉响警报的概率 $P(B)$ 是多少?雷达正确检测且飞机飞过的概率 $P(A|B)$ 是多少
解答:
因为 $P(B) = P(A)P(B|A) + P(A^c)P(B|A^c) = 0.050.99 + 0.950.1=0.1145$
已知 $P(B|A)$ 和 $P(A)$ 由条件概率定义可知 $P(A \cap B) = P(B|A) P(A) = 0.99 0.05 = 0.0495$
所以 $P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{0.0495}{0.1145} = 0.34$
所以,雷达拉响警报,告知我们来了飞机的概率只有 $0.34$ 也就是说,这个雷达其实蛮劣质的。
1.3 条件概率的一些法则
乘法法则
根据条件概率的定义,我们可以知道 $P(A \cap B) = P(A) P(B|A)$
那么如何求 $P(A \cap B \cap C)$ ?
简单,根据定义 $P(A \cap B \cap C) = P(A \cap B) P(C |A \cap B) = P(A) P(B|A) P(C |A \cap B) $
可以推广到 $n$ 个事件同时发生的情况。
用数学公式表示就是:
$$P(A_1 \cap A_2 \cap A_3 … \cap A_n) = P(A_1) \prod_{i=2}^n P(A_i | A_1 \cap … \cap A_i-1)$$
全概率公式
介绍全概率公式之前,我们需要介绍一个概念,就是完备事件组
若事件组 $(A_1, …A_i, …A_n)$ 满足条件
$A_i, i=1,2, …, n$ 两两互不相容,且 $P(A_i) > 0$
$\sum_{i=1}^n A_i = \Omega$
则称 $(A_1, …A_i, …A_n)$ 是 $\Omega$ 的一个完备事件组,也称为 $\Omega$ 的一个分割。
那么,在已知 $(A_1, …A_i, …A_n)$ 是一个完备事件组的时候,我们有
$$P(B) = \sum_{i=1}^n P(A_i) P(B|A_i)$$
也就是说,对于事件 $B$ 而言,我们就算不知道它发生的概率,但是我们知道事件 $A_i$ 发生的概率和事件 $A_i$ 发生的时候,事件 $B$ 发生的概率,我们一样可以通过全概率公式,求出事件 $B$ 的概率。
贝叶斯公式
在已知 $(A_1, …A_i, …A_n)$ 是一个完备事件组的时候,我们有
$$P(A_i|B) = \frac{P(A_i \cap B)}{P(B)}= \frac{P(A_i) P(B|A_i)}{\sum_j P(A_j) P(B|A_j)}$$
贝叶斯公式在于能够使用一种系统的方法来融合新的证据
比如,我们本来只知道事件 $A_i$ 发生的概率,但是在事件 $B$ 发生之后,我们可以得到新的概率 $P(A_i|B)$
2. Independence(独立)
2.1 Independence of two events
独立的直觉定义是 $P(A|B) = P(A)$ 也就是说事件 $B$ 的发生,并没有为我们推断事件 $A$ 发生的概率提供有用的信息。
给出独立的定义:
$$P(A \cap B) = P(A) P(B)$$
满足上式的两个事件就是独立事件。
牢记独立的定义是 $P(A \cap B) = P(A) P(B)$
那么如果 $A$ 和 $B$ 是独立的, $A$ 和 $B^c$ 是否独立呢?
我们可以从定义出发:
由 $A = (A \cap B) \cup (A \cap B^c)$ 可知。
因为 $A$ 和 $B$ 独立,所以,可以换成如下表示
$P(A) = P(A \cap B) + P(A \cap B^c) = P(A) P(B) + P(A \cap B^c)$
左移变化得到
$P(A \cap B^c) = P(A) - P(A) P(B) = P(A) (1 - P(B)) = P(A)P(B^c)$
2.2 Conditional independence
条件独立:给定一个事件 $C$, 条件独立就是 $P(A \cap B | C) = P(A|C) P(B|C)$ 。这时候 $A$ 和 $B$ 可以不是独立的。但是在事件 $C$ 发生的时候, $A$ 和 $B$ 独立。
条件可能影响独立
比如,现在有两个硬币 $A$ 和 $B$,每个硬币有 $H$(人像) 和 $T$ (数字)两面。
给定概率 $P(H|A) = 0.9$, $P(H|B) = 0.1$
请比较 $P(toss 11 = H)$ 和 $P(toss 11 = H | first 10 tosses are heads)$
对于第一种情况,由于我们不知道选取的硬币是 $A$ 还是 $B$
所以, $P(toss 11 = H) = 0.5 0.9 + 0.5 0.1 = 0.5$
对于第二种情况,因为前10次投掷都是 head ,所以,我们大概率选取了硬币 A 作为实验硬币。所以 $P(toss 11 = H | first 10 tosses are heads) \approx 0.9$
2.3 Independence of a collection of events
事件 $A_1, A_2, A_3, … A_n$ 相互独立,当且仅当 $P(A_i \cap A_j \cap … \cap A_m) = P(A_i) P(A_j) P(A_3) P(A_m)$ 对于任意的不相同的下标 $i, j, …, m$ 都成立。
比如 $n=3$ 的时候。
$A_1, A_2, A_3$ 相互对立,当且仅当
$P(A_1 \cap A_2) = P(A_1) \cdot P(A_2)$
$P(A_1 \cap A_3) = P(A_1) \cdot P(A_3)$
$P(A_2 \cap A_3) = P(A_2) \cdot P(A_3)$
$P(A_1 \cap A_2 \cap A_3) = P(A_1) \cdot P(A_2) \cdot P(A_3)$
上述式子成立,则 $A_1, A_2, A_3$ 相互对立。
2.4 Pairwise independence
两两独立:设 $A_1, A_2, A_3, … A_n$ 是 $n$ 个事件,若其中任意两个事件之间均相互独立,则称 $A_1, A_2, A_3, … A_n$ 两两独立。
注:相互独立一定两两独立、两两独立不一定相互独立。
比如现在有一个公平的骰子,正反概率各 $0.5$ ,事件 $A$ 是第一次扔到正面; 事件 $B$ 是第二次扔到正面; 事件 $C$ 是第一次和第二次的情况相同。
那么 $P(A) = \frac{1}{2}$, $P(B) = \frac{1}{2}$, $P(C) = \frac{1}{2}$
且,事件 A 和事件 C 同时发生的概率为 $P(A \cap C) = \frac{1}{4} = P(A) P(C)$
事件 B 和事件 C 同时发生的概率为 $P(B \cap C) = \frac{1}{4} = P(B) P(C)$
事件 A 和事件 B 同时发生的概率为 $P(A \cap B) = \frac{1}{4} = P(A) P(B)$
但是 $P(A, B, C) = \frac{1}{4} \ne P(A) P(B) P(C) = \frac{1}{8}$
另一个角度来说,当我们已知
A, B 发生 C 发生的概率是 $P(C | A, B) = 1 \ne P(C)$
所以,相互独立(independence)和两两独立(Pairwise independence)是两个完全不同的概念。
2.5 条件对情况的影响
例子:
国王来自一个有着两个孩子的家庭,那么他们家庭中另外一个小孩是女性的概率是多少?
直觉上,我们会认为这个概率是 0.5 但是真是这样么?
这其实是一个条件概率。“一个家庭有两个小孩” 一共有4中情况 男男、男女、女男、女女。
现在,我们已知有一个小孩是男孩,求另外一个小孩是女孩的概率。
也就是说,这时候,整体的情况应该是 男男、男女、女男 。我们需要把 女女的概率排除,因为不存在这种情况。
所以,这时候的概率应该是 $\frac{2}{3}$
2.6 习题
- Conditional probability example. We roll two fair 6-sided dice. Each one of the 36 possible outcomes is assumed to be equally likely.
(a) Find the probability that doubles are rolled (i.e., both dice have the same number).
(b) Given that the roll results in a sum of 4 or less, find the conditional probability that doubles are rolled.
(c) Find the probability that at least one die roll is a 6.
(d) Given that the two dice land on different numbers, find the conditional probability that at least one die roll is a 6.
Tips: 如果感觉这样的题目分析起来麻烦,可以通过画坐标点的方式来解决。
解:
(a) 设事件 $A$ 表示两次投掷数目相同。$P(A) = \frac{1}{6}$
(b) 设事件 $B$ 表示两次投掷的数值和小于等于4. 则 $P(A|B) = \frac{1}{3}$
(c) 设事件 $C$ 表示两次投掷中至少有一个骰子投到了6. 则 $P(C) = \frac{11}{36}$
(d) 设事件 $D$ 表示两次投掷都投掷到了不同的数字. 则 $P(C|D) = \frac{1}{3}$
- A chess tournament problem. This year’s Belmont chess champion is to be selected by the following procedure. Bo and Ci, the leading challengers, first play a two-game match. If one of them wins both games, he gets to play a two-game second round with Al, the current champion. Al retains his championship unless a second round is required and the challenger beats Al in both games. If Al wins the initial game of the second round, no more games are played.
Furthermore, we know the following:
∙ The probability that Bo will beat Ci in any particular game is 0.6.
∙ The probability that Al will beat Bo in any particular game is 0.5.
∙ The probability that Al will beat Ci in any particular game is 0.7.
Assume no tie games(平局) are possible and all games are independent.
1.Determine the a priori probabilities that
(a) the second round will be required.
(b) Bo will win the first round.
(c) Al will retain his championship this year.
2.Given that the second round is required, determine the conditional probabilities that
(a) Bo is the surviving challenger.
(b) Al retains his championship.
3.Given that the second round was required and that it comprised only one game, what is the conditional probability that it was Bo who won the first round?
Tips: 如果感觉这样的题目分析起来麻烦,可以通过画树结构的方式来解决。
解:
(1)
设事件 A 表示 “需要进行第二轮比赛”
也就是说 Bo 赢了 Ci 两把或者 Ci 赢了 Bo 两把。
$P(A) = 0.6 0.6 + 0.4 0.4 = 0.52$
设事件 B 表示 “Bo 赢了第一轮”
$P(B) = 0.6 * 0.6 = 0.36$
设事件 C 表示 “Ai 继续成为冠军”
我们可以从反面来求 $P(C^c) = 0.6 0.6 0.5 0.5 + 0.4 0.4 0.3 0.3 = 0.1044$
那么 $P(C) = 1 - P(C^c) = 0.8956$
(2)
设事件 D 表示 “Bo 成为第二轮挑战者”
$P(D|A) = \frac{P(A \cap D)}{P(A)} = \frac{0.6 * 0.6}{0.52} = 0.6923$
所以
$P(C|A) = \frac{P(A \cap C)}{P(A)} = \frac{0.6 0.6 0.5 + 0.6 0.6 0.5 0.5 + 0.4 0.4 0.7 + 0.4 0.4 0.3 0.7}{0.52} = 0.7992$
(3)
设事件 E 表示 “需要进行第二轮比赛,且只进行了一场”
$P(E) = 0.6 0.6 0.5 + 0.4 0.4 0.7 = 0.292$
$P(B|E) = \frac{P(B \cap E)}{P(E)} = \frac{0.6 0.6 0.5}{0.292} = 0.6164$
- A coin tossing puzzle. A coin is tossed twice. Alice claims that the event of getting two Heads is at least as likely if we know that the first toss is Heads than if we know that at least one of the tosses is Heads. Is she right? Does it make a difference if the coin is fair or unfair? How can we generalize Alice’s reasoning?
解:
设事件 A 表示 “投掷两次都是正面”
事件 B 表示 “第一次投掷是正面”
事件 C 表示 “至少有一次是正面”
同时,设投掷为正面的概率为 $p$
所以,根据已知条件我们有 $P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{p * p}{p} = p$
$P(A|C) = \frac{P(A \cap C)}{P(C)} = \frac{p p}{p} = \frac{p p}{p(1-p) + p*p + p(1-p)} = \frac{p}{2-p}$
所以,在骰子是公平,也就是 $p=0.5$ 的时候。 $P(A|B) = 0.5$, $P(A|C) = 0.33$ 所以是正确的猜测。当然在不公平的时候,也是正确的。
更加一般的形式是:
假设现在有事件 A、B、C、D、E,其中 $C = A\cap B$, $D = A$, $E = A\cup B$
已知, 1) $D \subset E$ 2) $c \cap D = C \cap E$ 那么有 $P(C|D) \geq P(C|E)$
因为 $E$ 的搜索范围比 $D$ 的大,所以分母就会更大。
- The Monty Hall problem. This is a much discussed puzzle, based on an old American game show. You are told that a prize is equally likely to be found behind any one of three closed doors in front of you. You point to one of the doors. A friend opens for you one of the remaining two doors, after making sure that the prize is not behind it. At this point, you can stick to your initial choice, or switch to the other unopened door. You win the prize if it lies behind your final choice of a door. Consider the following strategies:
Stick to your initial choice.
Switch to the other unopened door.
You first point to door 1. If door 2 is opened, you do not switch. If door 3 is opened, you switch.
Which is the best strategy?
中文译文:
假设你在参加一个游戏节目,有三扇门,两扇后面是羊 ,一扇后面是车。你选了一扇门,再打开之前,你得朋友打开了你没选的其中一扇门,那个后面是羊,那么这时候你是继续坚持你选的门还是换到另一扇门赢到车的几率大?
Tips: 如果感觉这样的题目分析起来麻烦,可以通过画表格的方式来解决。
解:
| choose | prize | open | stay | switch |
|---|---|---|---|---|
| 1 | 1 | 2 或 3 | 中奖 | 未中奖 |
| 1 | 2 | 3 | 未中奖 | 中奖 |
| 1 | 3 | 2 | 未中奖 | 中奖 |
| 2 | 1 | 3 | 未中奖 | 中奖 |
| 2 | 2 | 1 或 3 | 中奖 | 未中奖 |
| 2 | 3 | 1 | 未中奖 | 中奖 |
| 3 | 1 | 2 | 未中奖 | 中奖 |
| 3 | 2 | 1 | 未中奖 | 中奖 |
| 3 | 3 | 1 或 2 | 中奖 | 未中奖 |
现在,让我们简单点思考。如果,我们不选择换门,这个问题其实可以等价于 “有三个门,只有一个门有奖,我们随机选择一个获奖的概率多大” 这时候,中奖的概率是 $\frac{1}{3}$。
如果,我们选择换门,我们如何计算概率,直接计算似乎不容易,那么我们求它的对立面,也就是 “换门输了的概率多大”。 什么情况下,换门会输呢? “只有当我们选择了正确的门的情况下,换门才会输”,而选择正确门的概率上面给出了是 $\frac{1}{3}$, 所以,这里换门赢的概率就是 $1 - \frac{1}{3} = \frac{2}{3}$。
所以,换门胜利的概率更高。更加形式化的描述如上面的表格所示。
表格中的数据告诉我们, stay 策略只在我们一开始选择正确的时候能获胜。但是 switch 策略在我们一开始选择错误的时候可以获胜。
那么现在考虑第三种策略。
You first point to door 1. If door 2 is opened, you do not switch. If door 3 is opened, you switch.
因为,我们已经选定了第一扇门,所以现在假设朋友打开第二扇门的概率是 $p$
那么,从上面的表格可以看出,我们中奖和不中奖的概率与 $p$ 有关。
中奖的概率是 $\frac{1}{3} p + \frac{1}{3}$
- A random walker. Imagine a drunk tightrope walker, who manages to keep his balance, but takes a step forward with probability p and takes a step back with probability (1−p).
(a) What is the probability that after two steps, the tightrope walker will be at the same place on the rope as where he started?
(b) What is the probability that after three steps, the tightrope walker will be one step forward from where he started?
(c) Given that after three steps he has managed to move ahead one step, what is the probability that the first step he took was a step forward?
解:
(a)
走两步有四种情况, 前前、后后、前后、后前。
$P(A) = 2p(1-p)$
(b)
走三步有八种情况, 前前前、前前后、前后前、前后后、后前前、后前后、后后前、后后后。
$P(B) = 3 p^2 (1-p)$
(c)
设事件 C 是 the first step he took was a step forward?
$P(C|B) = \frac{P(C \cap B)}{P(B)} = \frac{2 p^2 (1-p)}{3 p^2 (1-p)} = \frac{2}{3}$
- Communication over a noisy channel. A source transmits a message (a string of symbols) over a noisy communication channel. Each symbol is 0 or 1 with probability p and 1−p, respectively, and is received incorrectly with probability ϵ0 and ϵ1, respectively (see the figure below). Errors in different symbol transmissions are independent.
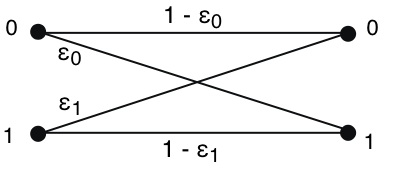
(a) What is the probability that the $k$th symbol is received correctly?
(b) What is the probability that the string of symbols $1011$ is received correctly?
(c) In an effort to improve reliability, each symbol is transmitted three times and the received string is decoded by majority rule. In other words, a 0 (or 1) is transmitted as 000 (or 111, respectively), and it is decoded at the receiver as a 0 (or 1) if and only if the received three-symbol string contains at least two 0’s (or 1’s, respectively). What is the probability that a 0 is correctly decoded?
(e) Suppose that the scheme of part (c) is used. What is the probability that a symbol was 0 given that the received string is 101?
解:
(a)
设事件 $A$ 表示第 $k$ 个标识被正确接收。
$P(A) = p(1-\epsilon_0) + (1-p)(1-\epsilon_1)$
(b)
设事件 B 表示 $1101$ 被正确接收
$P(B) = (1-\epsilon_1) (1-\epsilon_0) (1-\epsilon_1) (1-\epsilon_1)$
(c)
设事件 C 表示一个 $0$ 被正确解码
$P(C) = (1-\epsilon_0)^3 + 3 \epsilon_0 (1-\epsilon_0)^2$
(e)
在 (c) 假设下求 $P(“0” | 101) = \frac{P(101|”0” ) P(“0”)}{P(101)}$
其中 $P(101) = P(“0”) P(101|”0”) + P(“1”)P(101|”1”)$
且 $P(“0”) = p$ 且 $P(“1”) = 1-p$
所以 $P(101|”0”) = (1-\epsilon_0) \epsilon_0^2$
$P(101|”1”) = (1-\epsilon_1)^2 \epsilon_1$
综上 $P(“0” | 101) = \frac{p(1-\epsilon_0) \epsilon_0^2}{ p (1-\epsilon_0) \epsilon_0^2 + (1-p) (1-\epsilon_1)^2 \epsilon_1 }$
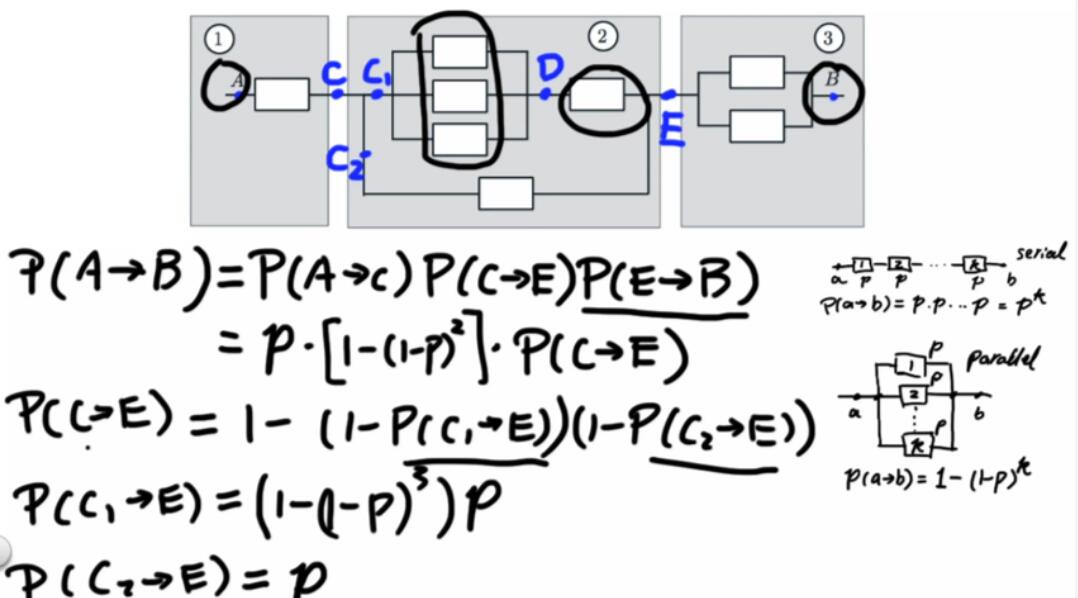
- Network reliability. An electrical system consists of identical components, each of which is operational with probability p, independent of other components. The components are connected in three subsystems, as shown in the figure. The system is operational if there is a path that starts at point A, ends at point B, and consists of operational components. What is the probability of this happening?
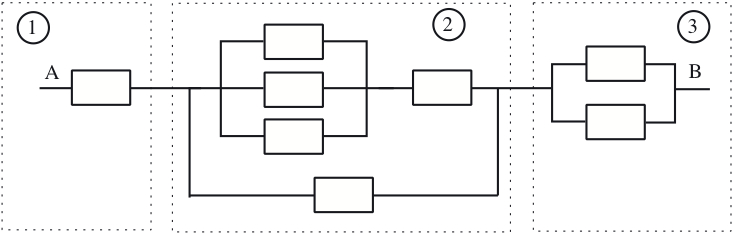
解:
思路是分而治之。考虑清楚情况就可以
$P = p [1-{(1-p)}^2] { 1 - (1-p) [1- p[1-{(1-p)}^3]] }$