Udacity《Reinforcement Learning》课程中内容的笔记
强化学习 (1)
引言
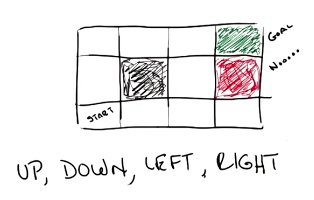
对于上图,你需要找到一条从 start 到 goal 的路径,其中黑色的线条和方格分别是墙和陷阱,你可以选择什么样的路径?
U, D, L and R for Up, Down, Left, and Right (respectively)
很显然,一个比较简单的方法就是 UURRR
现在,我们给出一个挑战,如果我们的 agent 行走的路线,并不会按照既定路线行走(也就是说它有 20% 的概率跑偏,比如我们要求它向上走,它有 80% 的几率向上走,也有 10% 的几率向左走,10% 的几率向右走) 。现在我们让这个 agent 按照路线 UURRR 去行走,它最终能走到 goal 的概率有多大?
从 start 走到 goal 的情况有两种,第一种是,全部按照既定行程走,则最后的结果是 $0.8^5=0.32768$ ; 第二种是,前四个出错了,第五个对了,则最后的结果是 $0.1^4∗0.8=0.0008$。 所以总计: $0.32768 + 0.0008 = 0.32776$
概述
与机器学习中概念对比
- 监督学习:给定多组 $(x,y)$ 拟合出一个Loss 最低的 $f(x)$
- 无监督学习: 给定多组 $x$ ,找到一组函数集可以联合描述 $x$ 的变化特性。
- 强化学习:与监督学习相似,给定多组 $(x,y)$ ,同时一个抉择向量 $z$ 。强化学习可以称之为监督学习的扩展,扩展了一套决策方案而非单一的梯度下降。
强化学习的定义:
- 提供了关于Decision Making在机器上的实现方案
- 基于计算机尝试不按既定规则的权利
- 通过 奖励函数 来使看似随机的函数行为变得可控
- 通过 延迟奖励 使得决策注重整体,而非局部最优
- 通过 回滚决策 对一系列决策进行判断,尝试寻找问题的所在
延迟奖励:强化学习的驱动是每次按规则给每个状态丢到另一个状态。但具体这个决策好或者不好,只有在之后的特定条件时才会知道。比如下棋,当经过60步后你赢的了棋局。这时你才明白这60步的决策是好是坏。
强化学习中的核心概念: Markov Decision Processes (MDP)
the property of Markov is Only present matters!
STATES(状态): $S$
ACTION(动作): $A(S)$, $A$
MODEL(模型): $T(S, a, \acute{S}) \sim P_r (\acute{S} | S, a)$
REWARD(奖励): $R(S)$, $R(S,a)$, $R(S,a,\acute{S})$
——————————————
POLICY(策略): $\pi (S) \to a$
状态就是用来描绘当前世界的环境的。 放在上面的例子中就是从 $(1, 1)$ 到 $(4, 3)$ 所组成的点的集合
动作可以看成是状态的函数(因为有时候在某些状态下,有些动作是允许的,有些动作是不允许的),或者一组动作。 在上面的例子中就是 U, D, R, L 四个动作。
模型描述的是你正在进行的博弈的规则。所以这个 function 具有三个变量 状态、动作、另一个状态。这个函数生成的是概率,也就是你从状态 $S$ 采取动作 $a$ 转换到状态 $\acute{S}$ 的概率
奖励在这里用了三个函数表示,它们的含义分别是:进入一个状态下的奖励、进入一个状态下并采取某个动作获得的奖励、在当前状态下采取某个动作进入到另一个状态下获得的奖励。
策略告知了我们在一个特定的状态中应该采取什么样的动作。 Policy就像一个老师,如果这个 Policy是最优的,它就告诉了我们在什么状态下应该做什么事。
所以,一个 MDP 由 问题 和 策略 组成!
STATES + ACTION + MODEL + REWARD = 问题
POLICY = 策略
MDP框架的核心是让程序关注在什么状态下,做什么比较好,是否会得到的奖励,所以,MDP的关键是奖励函数的设置,最终规则集合包含了一系列奖惩措施
奖励的重要性:
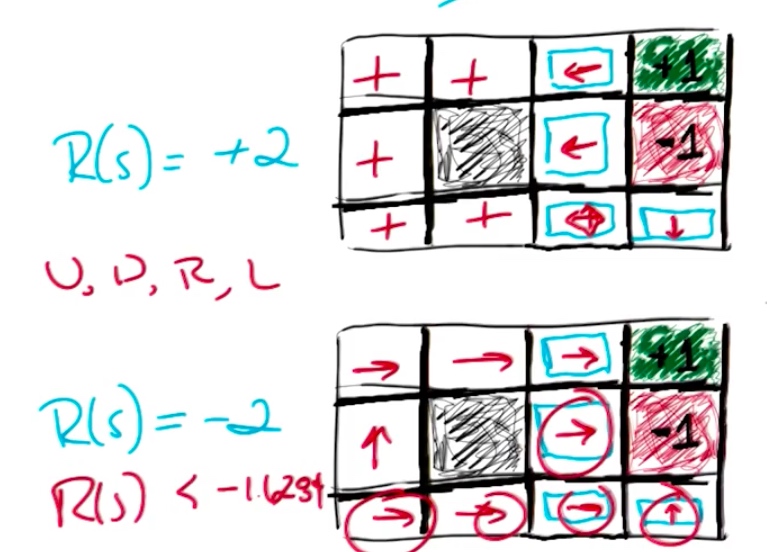
这是一个关于默认奖励不同的情况的两个例子,上面的区块默认奖励为+2,下面的默认奖励为-2。
对于上面的而言,奖励为正值。为了能获得到更多的奖励,我们不能让程序进入停止游戏区间,最好的办法就是撞墙(不断的停留原地所以获得奖励)
对于下面的区间,由于奖励为负值,我们需要尽快的离开游戏。右下角的方向为上的原因是,如果当前为其他方向,那么肯定会有至少一个-2出现在奖励序列里。所以最好的方法是:直接终止,取得那个-1的红色区间
通过这个例子可以看出,当奖励函数不同,强化学习最后得到的规则集合也是截然不同的。
所以,定义一个好的 reward 非常的重要!
偏向稳定性
定义
如果有两个时间序列 $A:s_0, s_1, s_2$ 与 $B:s_0, \acute{s_1}, \acute{s_2}$ ,如果 $A>B$ 则 $A, B$ 的去掉相同元素的子序列$s_0$, 仍然满足$s_1, s_2 > \acute{s_1}, \acute{s_2}$。我们称这种现象为偏向稳定性。
偏向稳定性与奖励序列
强化学习中,奖励是一个序列性的问题,也就是状态序列。学习的目的是希望最后能得到的总奖励最高。但请一定要注意时序的长短问题,即时间长度是否无限。
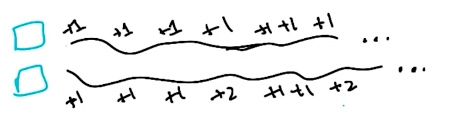
看上面的例子,如果问当上面情况一直重复时,哪个会更好?
答案是:两者都一样
因为,时间长度是无限,那么无论是上面的情况还是下面的情况,最终的结果都是 $+\infty$ 无法比较。
显然在无限时间内,讨论不受控制的没有负奖励的两个奖励序列的区别是无意义的
但是如上文单独讨论的一个序列的奖励大小也是无意义的。因为无穷大不是一个数。
这时我们就需要对无限增长的正奖励一个界定空间,即折扣期望
折扣期望
对面上面例子,在无限情况下,奖励的期望(在奖励为正的情况下)应该是
$$\sum_{t=0}^{\infty} R(S_t) = + \infty$$
如果,我们给这个奖励添加一个参数 $0 \leq \gamma < 1$,用如下形似表示:
$$\sum_{t=0}^{\infty} \gamma^t R(S_t)$$
此时当 $t$ 达到一定数量时,上式的值会停留在一个 $R_{max}$ 上。
会有(将那个式子当成等比数列看待)
$$\sum_{t=0}^{\infty} \gamma^t R(S_t) \leq \sum_{t=0}^{\infty} \gamma^t R_{max} = \frac{R_{max}}{1 - \gamma}$$
所以,上式就是奖励的无穷总和的泛化,我们称之为折扣期望
意义(这里的解释比较抽象,不好理解,建议观看原始视频,地址在这)
让获得的奖励具有边界。这里实际是将 $R_{max}$ 值直接类比为无穷大
折扣期望级数加和序列退化为等比序列
等比数列又允许我们使用无穷多的数字跟在奖励值后做乘积,但结果的是一个又穷的数字
允许我们在有穷的时间接触到无穷大
使之前的无穷时域具有了有穷性。
策略(Policy)
效用
最优策略是 $\pi^*$,这个最优策略应该可以最大化我们的长期期望奖励。
$$\pi^* = arg \max \limits_{\pi} E[\sum_t \gamma^t R(S_t) | \pi]$$
决策的效用的形式如下所示(可以这样理解,我们从某个状态开始,状态策略的效用就是那之后所发生的所有事,也就是那之后得到的奖励的期望):
$$U^{\pi} (S) = E[\sum_t \gamma^t R(S_t) | \pi, s_0 = s]$$
这里需要强调的是 $R(S) \neq U^{\pi} (S)$, 奖励给以我们的是及时的回报,而效用给以我们的是长期的反馈
- $R(s)$ 是在 $S$ 点状态时,得到的瞬时奖励
- $U(s)$ 是在 $S$ 点起遵循一种决策后,将得到的长期奖励的期望。也就是从 $S$ 点开始将获得所有奖励的和
举一个例子:
比如上大学会花费6000元,所以,在你选择上大学的时候,你会的回报是 -6000, 但是当你大学毕业之后,你找到了一份 12000 的工作,这个时候你的回报就是 +12000,因此,你选择上大学之后你的 reward 可能是 +6000, 但是你不选择上大学你的 reward 可能是 0.
所以,效用(utilites) 说明了所有延迟奖励的意义所在。
通过效用定义最优策略
$$\pi^* (S) = arg \max \limits_{a} \sum_{\acute{S}} T(S, a, \acute{S}) U(\acute{S})$$
这个公式的含义是从状态 $S$ 开始,寻找所有可以从 $S$ 到 $\acute{S}$ 的 action $a$,并且求和,这就是在状态 $S$ 下的最优策略,唯一的一个问题就是,在上面的定义中,我们并不知道 $U(\acute{S})$。
于是我们可以定义 $U(S) = U^{\pi^*} (S)$ 。
所以,这样最优策略的解释就清晰了 —— 就是对于每一个状态,返回的动作都能够最大化我的期望效用。
然后,效用可以表示成:
$$U(s) = R(s)+\gamma argmax_a \sum_{s’}{T(s,a.s’)U(s)}$$
也就是当前 $s$ 状态的奖励 $R(s)$ 加上 $s’$ 状态的折扣效用值。
这个 $U(s)$ 也被称之为贝尔曼(Bellman)方程, 该方程是求解 MDP 与强化学习的关键方程,它定义了某个状态中的真实价值。整个MDP都在这个方程中被提及了~
寻找策略
如何求解下面的式子:
$$U(s) = R(s)+ \gamma max_a \sum_{s’}{T(s,a.s’)U(s)}$$
假设我们有 $N$ 个状态,那么应该也就会有 $N$ 个方程(因为每个方程都表示一个状态的转移)
那么有多少个未知数呢? 因为 $R$ 已知, $T$ 已知,剩下不知道的就是 $U$
所以,我们需要求解的就是 N 个 N 元方程。
普通的矩阵线性变换的解法并不适用于这里,因为那个 $max$
所以,我们可以采取迭代的方式。
- 1.从任意效用开始
- 2.基于它们邻近的状态更新这些效用
- 3.重复操作2,直到收敛(??我不太确定这里的意思是不是收敛)
所以,上面的操作合起来用一个式子表示就是:
$$\hat{U}_{t+1} (s) = R(s) + \gamma \max_a \sum_{\acute{s}} T(s, a, \acute{s}) \hat{U}_{t} (\acute{s})$$
OK,现在让我们做一道练习来巩固一下这个迭代求效用的概念。
迭代求效用的习题

我们需要求状态 $x$ 处的效用,已知 $\gamma = \frac{1}{2}$, 除了两个吸收态的奖励分别是 $+1$ 和 $-1$,剩下状态的奖励都是 $R(s)=-0.04$ 且 $U_0 (S) = 0$,求状态 $x$ 的第一次迭代效用 $U_1 (x)$ 和第二次迭代效用 $U_2 (x)$
Tips: 每个 action 成功的概率只有 0.8
对于 $x$ 来说,第一次迭代,除了 $+1$ 那个状态可以得到最高收益,别的状态的收益都是 -0.04,所以应该采取的措施就是向右走。
所以 $U_1 (x) = -0.04 + \frac{1}{2} [0 0.1 + 0 0.1 + 1 * 0.8] = 0.36$
如果,需要求 $U_2(x)$ ,应该先知道 $x$ 下方的状态的效用。该状态最好的 action 就是向左撞墙,这样可以避免掉落到右侧的 -1 之中,所以,这个效用可以用上述的式子计算 $-0.04 + \frac{1}{2} [0 0.1 + 0 0.1 + 0 * 0.8] = 0.04$
于是,我们可以接着求出 $U_2(x)$。首先,得肯定的是,第二次的 action 肯定还是向右走,并且此时,我们的效能并不全是0. $U_2 (x) = -0.04 + \frac{1}{2} [0.1 0.36 + 0.1 -0.04 + 0.8 * 1] = 0.376$.
策略迭代
步骤:
- 从一个随机的规则 $\pi_0$ 开始
- 给定 $\pi_t$ 计算 $U_t = U^{\pi_t}$ 作为规则的评价
- 提升规则:$\pi_{t+1} = arg \max \limits_a \sum{T(s,a,s’)U_t(s’)}$
计算 $U_t$ 我们应该想到利用 Bellman 等式
$$U_t (s) = R(s) + \gamma \sum_{\acute{s}} T(s, \pi_t(s), \acute{s}) U_t (\acute{s})$$
- 评估时假定当前为最优决策,所以 $s$ 的状态就直接由最优决策决定
- 这里我们有 n 个未知数,n 个方程。所以有唯一解
Bellman 函数与强化学习
为了避免糊涂,这里强调一下,下面表述中的价值等价于上面表述中的效能
对于 Bellman 等式,我们已知的是
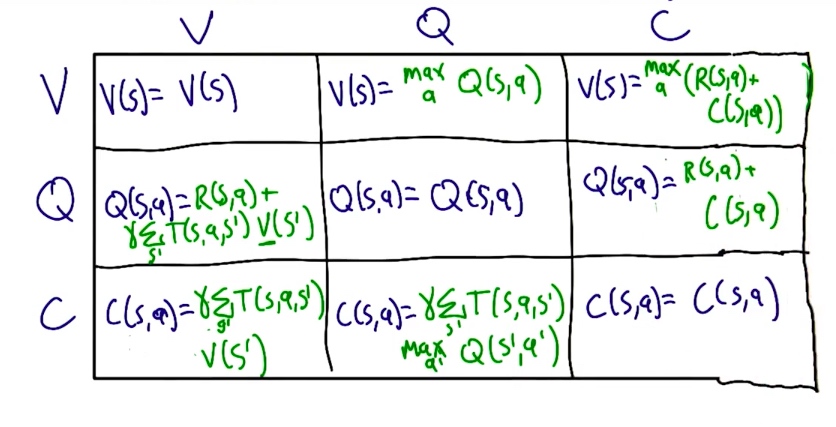
$$V(s_1) = \max_{a_1} (R(s_1,a_1)+\gamma \sum_{s_2}T(s_1,a_1,s_2)V(s_2))$$
我们称该式为 value 层面的 Bellman Function ,在强化学习中这是重要的函数
我们将 $max$ 中的内容看做一个整体,经过变换可得到
$$Q(s,a) = R(s,a)+\gamma\sum_{s’}T(s,a,s’) \max_{a’} (Q(s’,a’))$$
我们称该式为 Quality 层面的 Bellman Function,在强化学习中这是重要的函数
为什么会出现 Q Bellman Function 呢?
做一个小结: V function 其实是从 max开始迭代计算; Q function 是从 R(s)开始迭代计算,那么我们是不是可以从 $\gamma$ 开始迭代计算呢?如果沿着这条思路走,我们就可以定义出 C function
$$C(s,a) = \gamma \sum_{s’}T(s,a,s’) \max_{a’} (R(s’,a’)+C(s’,a’))$$
C V Q 之间的关系